Logistic regression

Lecture 17

John Zito

Duke University
STA 199 Spring 2025

2025-03-25

While you wait…

• Go to your ae project in RStudio.

• Make sure all of your changes up to this point are committed and pushed, i.e., there’s nothing left in your Git pane.

• Click Pull to get today’s application exercise file: ae-13-spam-filter.qmd.

• Wait till the you’re prompted to work on the application exercise during class before editing the file.

Thus far…

We have been studying regression:

• What combinations of data types have we seen?

• What did the picture look like?

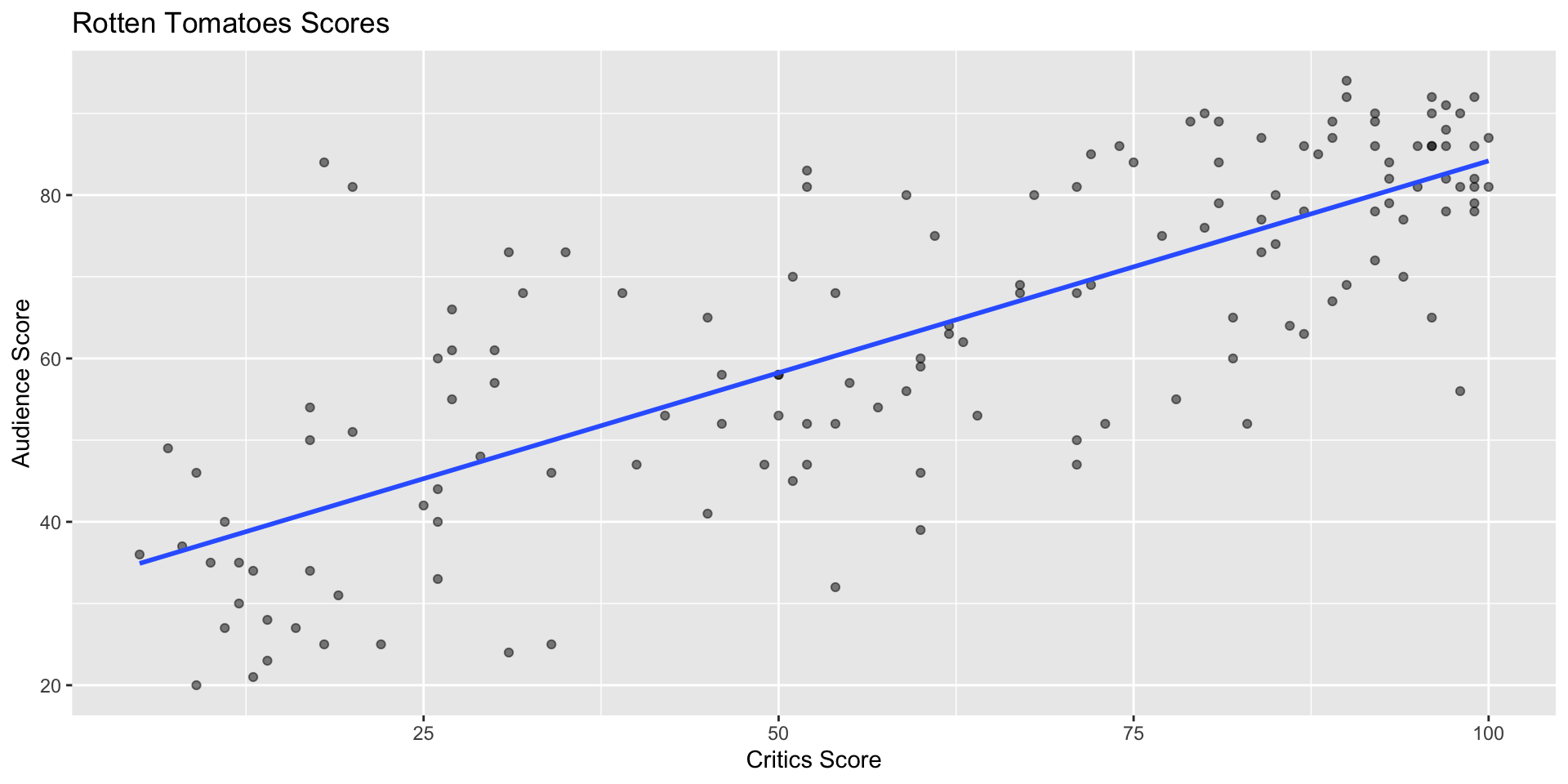
Recap: simple linear regression

Numerical response and one numerical predictor:

Recap: simple linear regression

Numerical response and one categorical predictor (two levels):

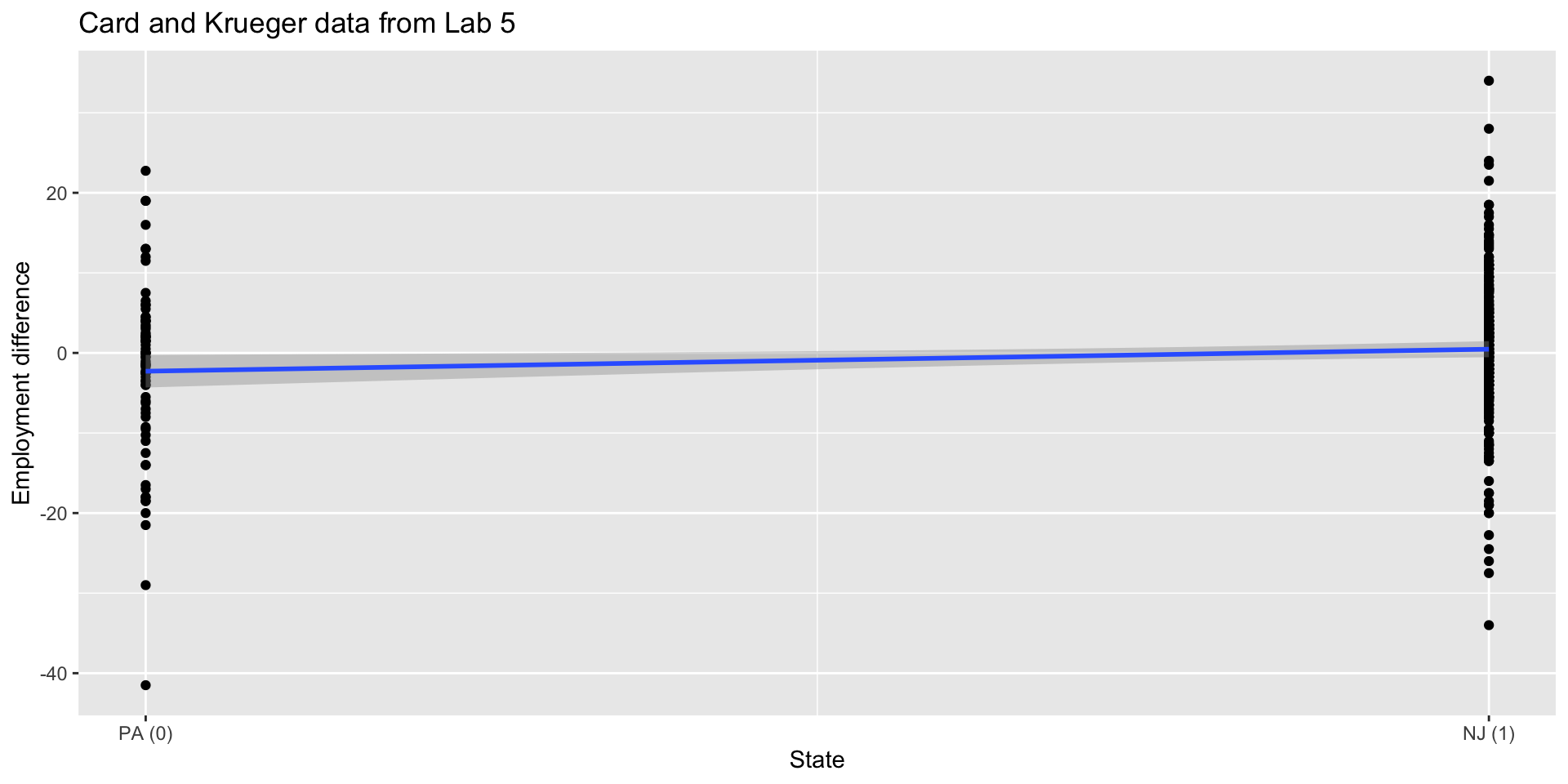
Recap: multiple linear regression

Numerical response; numerical and categorical predictors:

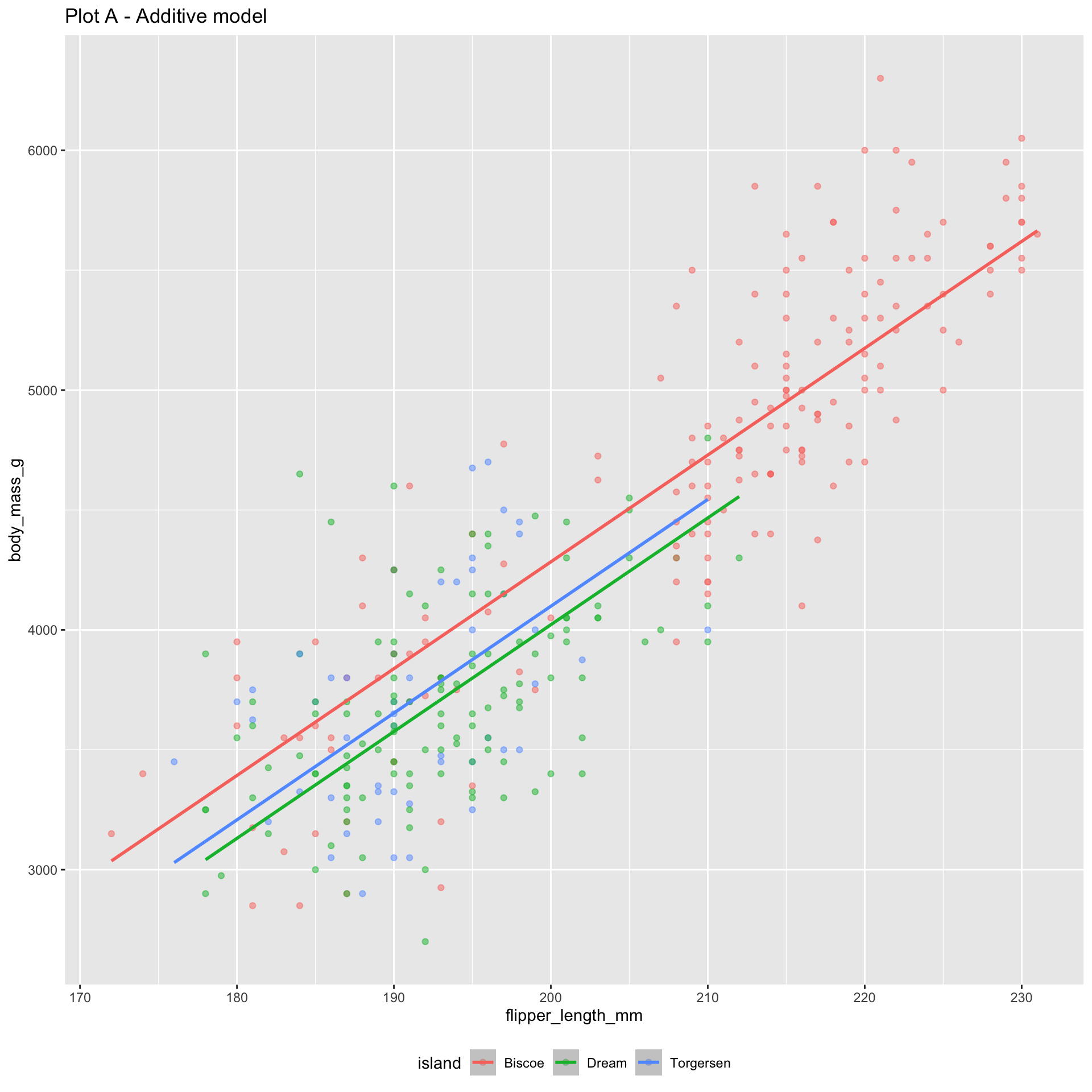
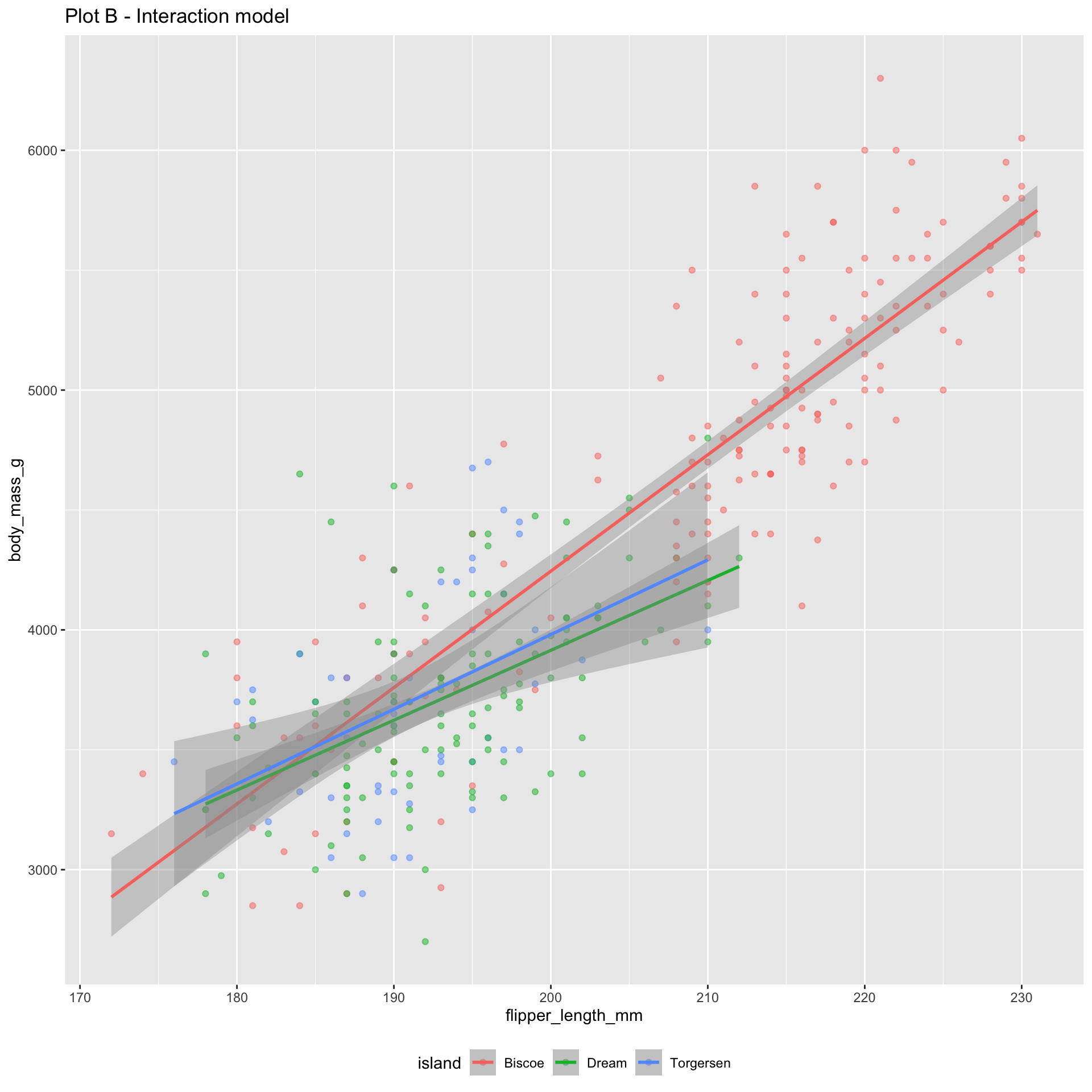
Today: a binary response

\[ y = \begin{cases} 1 & &&\text{eg. Yes, Win, True, Heads, Success}\\ 0 & &&\text{eg. No, Lose, False, Tails, Failure}. \end{cases} \]

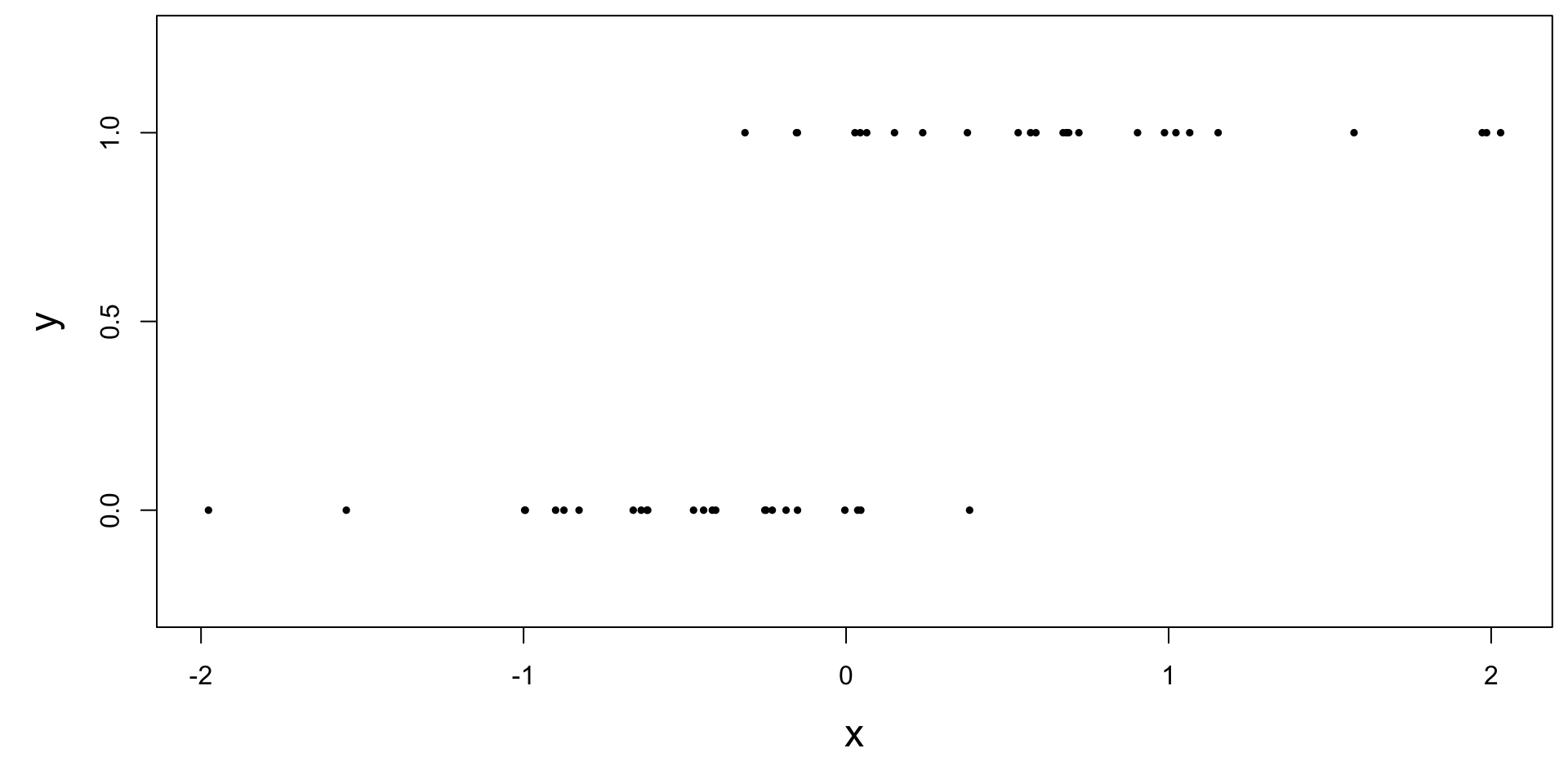
Who cares?

If we can model the relationship between predictors (\(x\)) and a binary response (\(y\)), we can use the model to do a special kind of prediction called classification.

Example: is the e-mail spam or not?

\[ \mathbf{x}: \text{word and character counts in an e-mail.} \]

\[ y = \begin{cases} 1 & \text{it's spam}\\ 0 & \text{it's legit} \end{cases} \]

Example: is it cancer or not?

\[ \mathbf{x}: \text{features in a medical image.} \]

\[ y = \begin{cases} 1 & \text{it's cancer}\\ 0 & \text{it's healthy} \end{cases} \]

Example: will they default?

\[ \mathbf{x}: \text{financial and demographic info about a loan applicant.} \]

\[ y = \begin{cases} 1 & \text{applicant is at risk of defaulting on loan}\\ 0 & \text{applicant is safe} \end{cases} \]

How do we model this type of data?

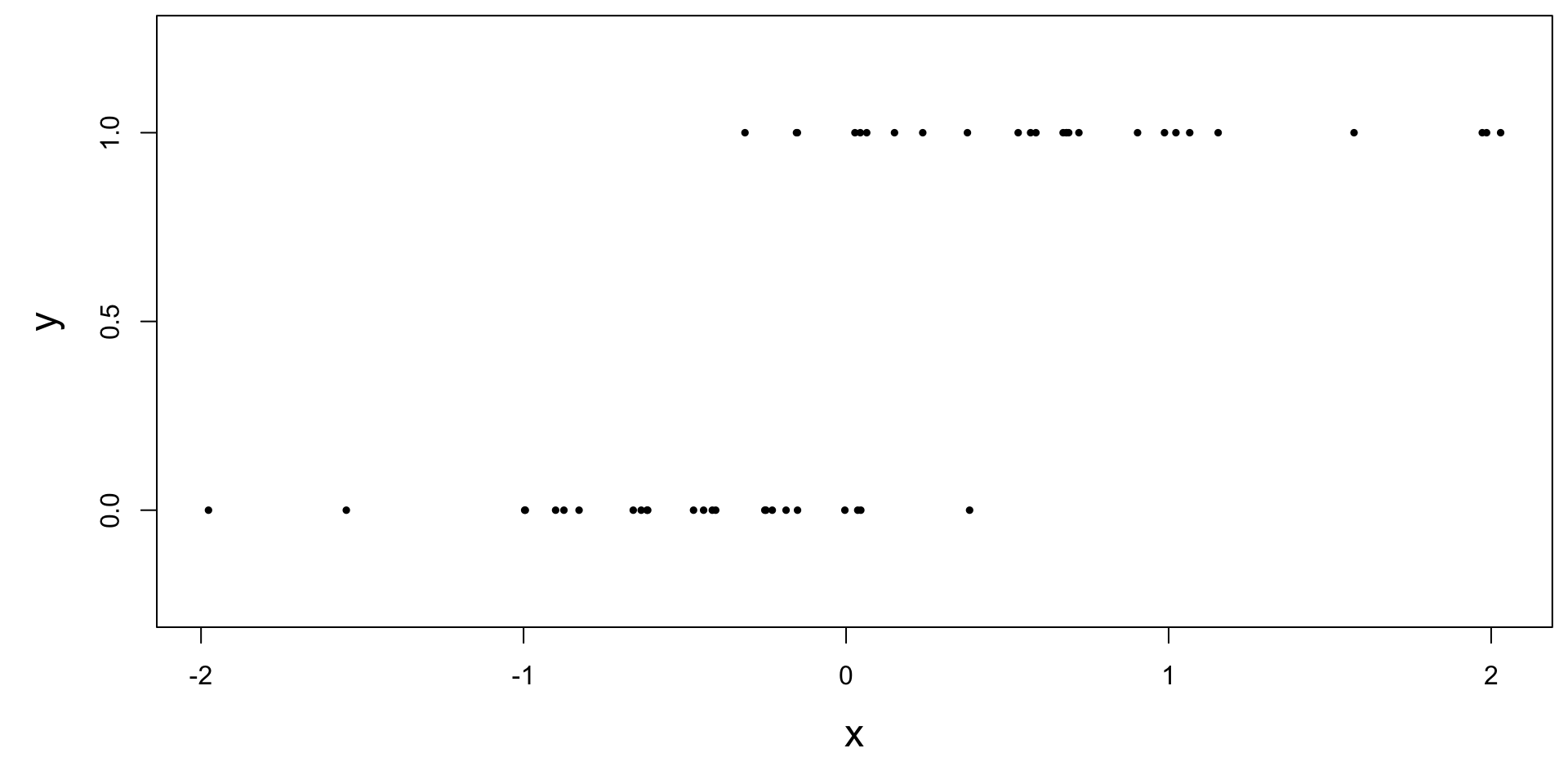
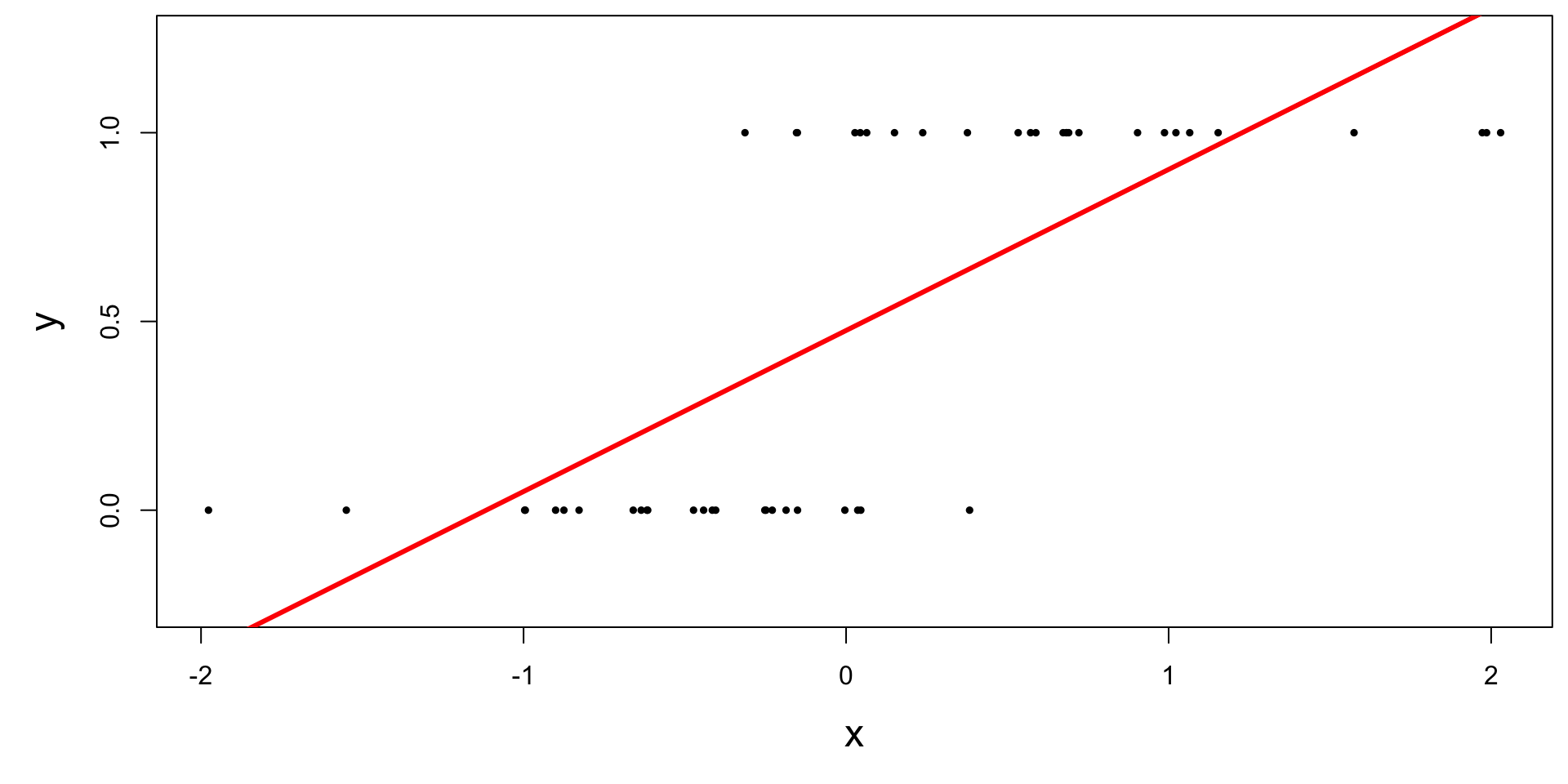
Straight line of best fit is a little silly

Instead: S-curve of best fit

Instead of modeling \(y\) directly, we model the probability that \(y=1\):

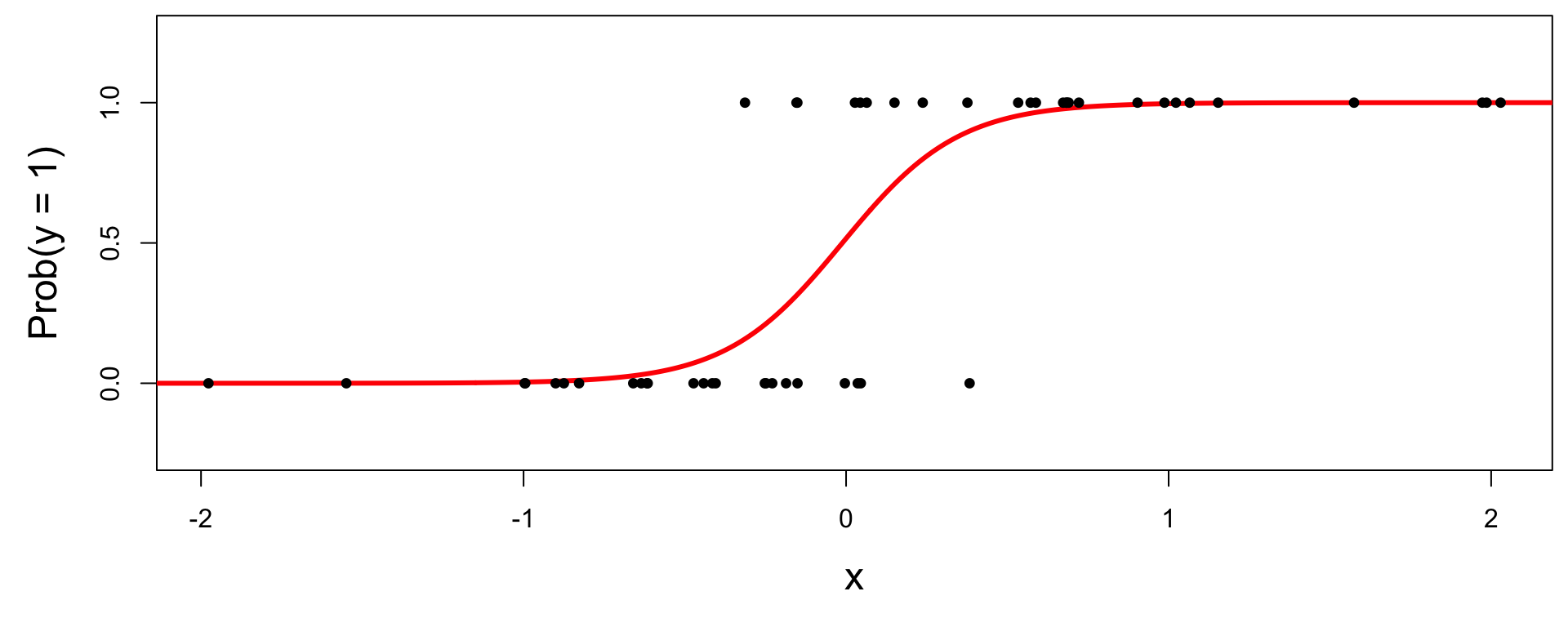
• “Given new email, what’s the probability that it’s spam?’’
• “Given new image, what’s the probability that it’s cancer?’’
• “Given new loan application, what’s the probability that they default?’’

Why don’t we model y directly?

• Recall regression with a numerical response:

  • Our models do not output guarantees for \(y\), they output predictions that describe behavior on average;

• Similar when modeling a binary response:

  • Our models cannot directly guarantee that \(y\) will be zero or one. The correct analog to “on average” for a 0/1 response is “what’s the probability?”

So, what is this S-curve, anyway?

It’s the logistic function:

\[ \text{Prob}(y = 1) = \frac{e^{\beta_0+\beta_1x}}{1+e^{\beta_0+\beta_1x}}. \]

If you set \(p = \text{Prob}(y = 1)\) and do some algebra, you get the simple linear model for the log-odds:

\[ \log\left(\frac{p}{1-p}\right) = \beta_0+\beta_1x. \]

This is called the logistic regression model.

Log-odds?

• \(p = \text{Prob}(y = 1)\) is a probability. A number between 0 and 1;

• \(p / (1 - p)\) is the odds. A number between 0 and \(\infty\);

“The odds of this lecture going well are 10 to 1.”

• The log odds \(\log(p / (1 - p))\) is a number between \(-\infty\) and \(\infty\), which is suitable for the linear model.

Probability to odds

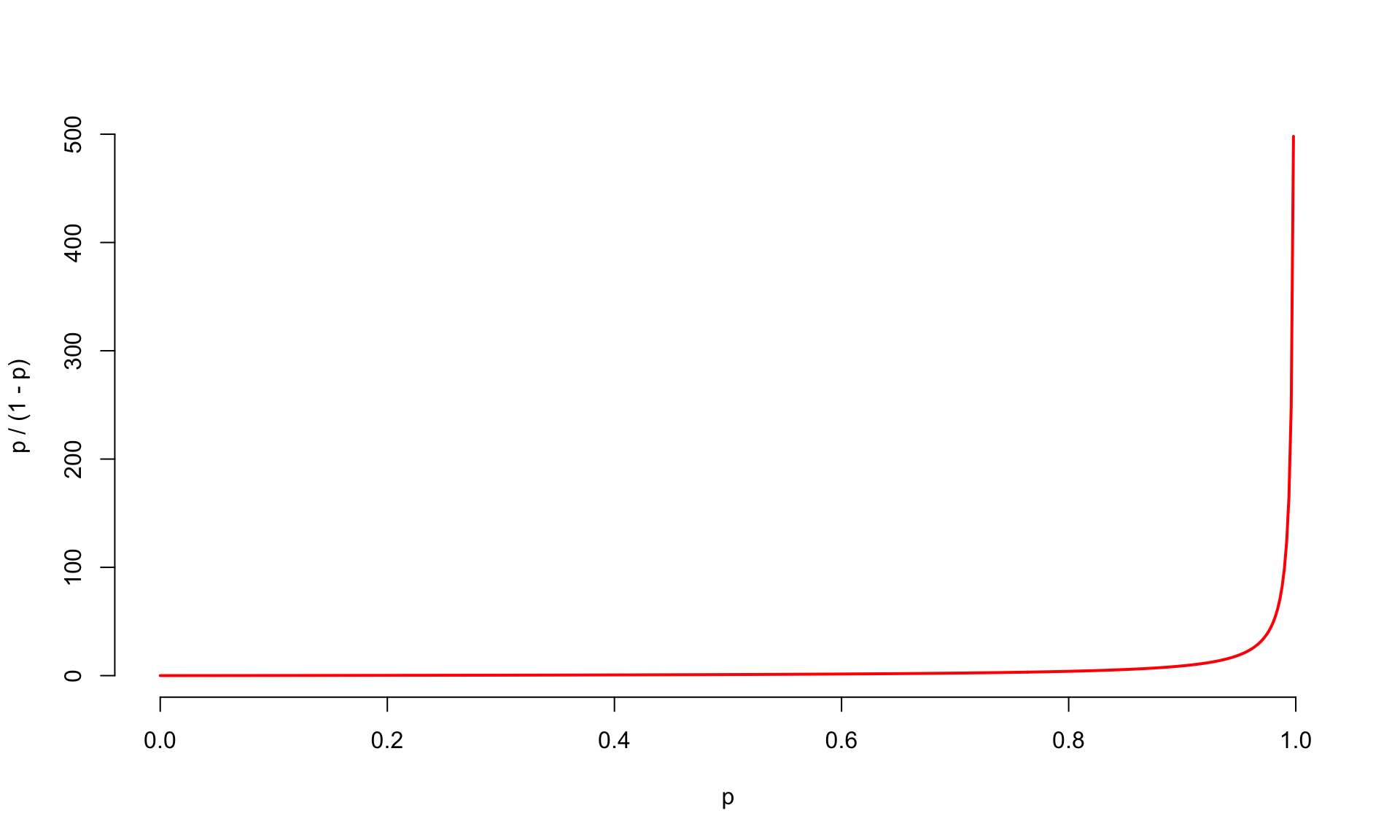
Odds to log odds

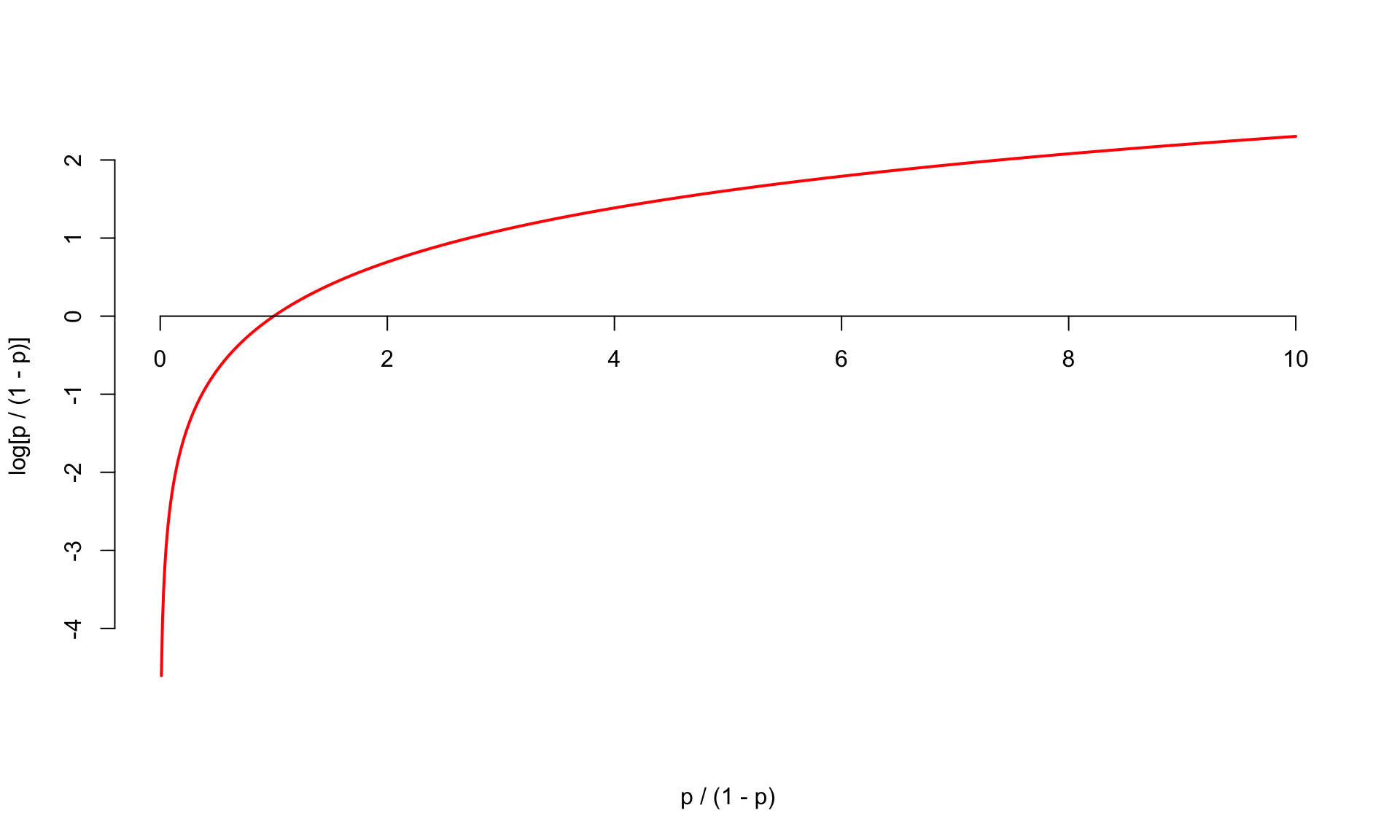
Logistic regression

\[ \log\left(\frac{p}{1-p}\right) = \beta_0+\beta_1x. \]

• The logit function \(\log(p / (1-p))\) is an example of a link function that transforms the linear model to have an appropriate range;

• This is an example of a generalized linear model;

Estimation

• We estimate the parameters \(\beta_0,\,\beta_1\) using maximum likelihood (don’t worry about it) to get the “best fitting” S-curve;

• The fitted model is

\[ \log\left(\frac{\widehat{p}}{1-\widehat{p}}\right) = b_0+b_1x. \]

Today’s data

email |> dplyr::select(c(spam, dollar, viagra, winner, password, exclaim_mess)) |> glimpse()

Rows: 3,921
Columns: 6
$ spam         <fct> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, …
$ dollar       <dbl> 0, 0, 4, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 2, 0, 5, 0, 0, …
$ viagra       <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, …
$ winner       <fct> no, no, no, no, no, no, no, no, no, no, no, no, no, no, n…
$ password     <dbl> 0, 0, 0, 0, 2, 2, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, …
$ exclaim_mess <dbl> 0, 1, 6, 48, 1, 1, 1, 18, 1, 0, 2, 1, 0, 10, 4, 10, 20, 0…

Fitting a logistic model

logistic_fit <- logistic_reg() |>
  fit(spam ~ exclaim_mess, data = email)

tidy(logistic_fit)

# A tibble: 2 × 5
  term          estimate std.error statistic p.value
  <chr>            <dbl>     <dbl>     <dbl>   <dbl>
1 (Intercept)  -2.27      0.0553     -41.1     0    
2 exclaim_mess  0.000272  0.000949     0.287   0.774

Fitted equation for the log-odds:

\[ \log\left(\frac{\hat{p}}{1-\hat{p}}\right) = -2.27 + 0.000272\times exclaim~mess \]

Interpreting the intercept

If exclaim_mess = 0, then

\[ \hat{p}=\widehat{P(y=1)}=\frac{e^{-2.27}}{1+e^{-2.27}}\approx 0.09. \]

So, an email with no exclamation marks has a 9% chance of being spam.

Interpreting the slope is tricky

Recall:

\[ \log\left(\frac{\widehat{p}}{1-\widehat{p}}\right) = b_0+b_1x. \]

Alternatively:

\[ \frac{\widehat{p}}{1-\widehat{p}} = e^{b_0+b_1x} = \color{blue}{e^{b_0}e^{b_1x}} . \]

If we increase \(x\) by one unit, we have:

\[ \frac{\widehat{p}}{1-\widehat{p}} = e^{b_0}e^{b_1(x+1)} = e^{b_0}e^{b_1x+b_1} = {\color{blue}{e^{b_0}e^{b_1x}}}{\color{red}{e^{b_1}}} . \]

A one unit increase in \(x\) is associated with a change in odds by a factor of \(e^{b_1}\). Gross!

Back to the example…

\[ \log\left(\frac{\hat{p}}{1-\hat{p}}\right) = -2.27 + 0.000272\times exclaim~mess \]

If we add one exclamation mark to the model, we predict the odds of an email being spam to be higher by a factor of \(e^{0.000272}\approx 1.000272\) on average.

Logistic regression -> classification?

Step 0: fit the model

Select a number \(0 < p^* < 1\):

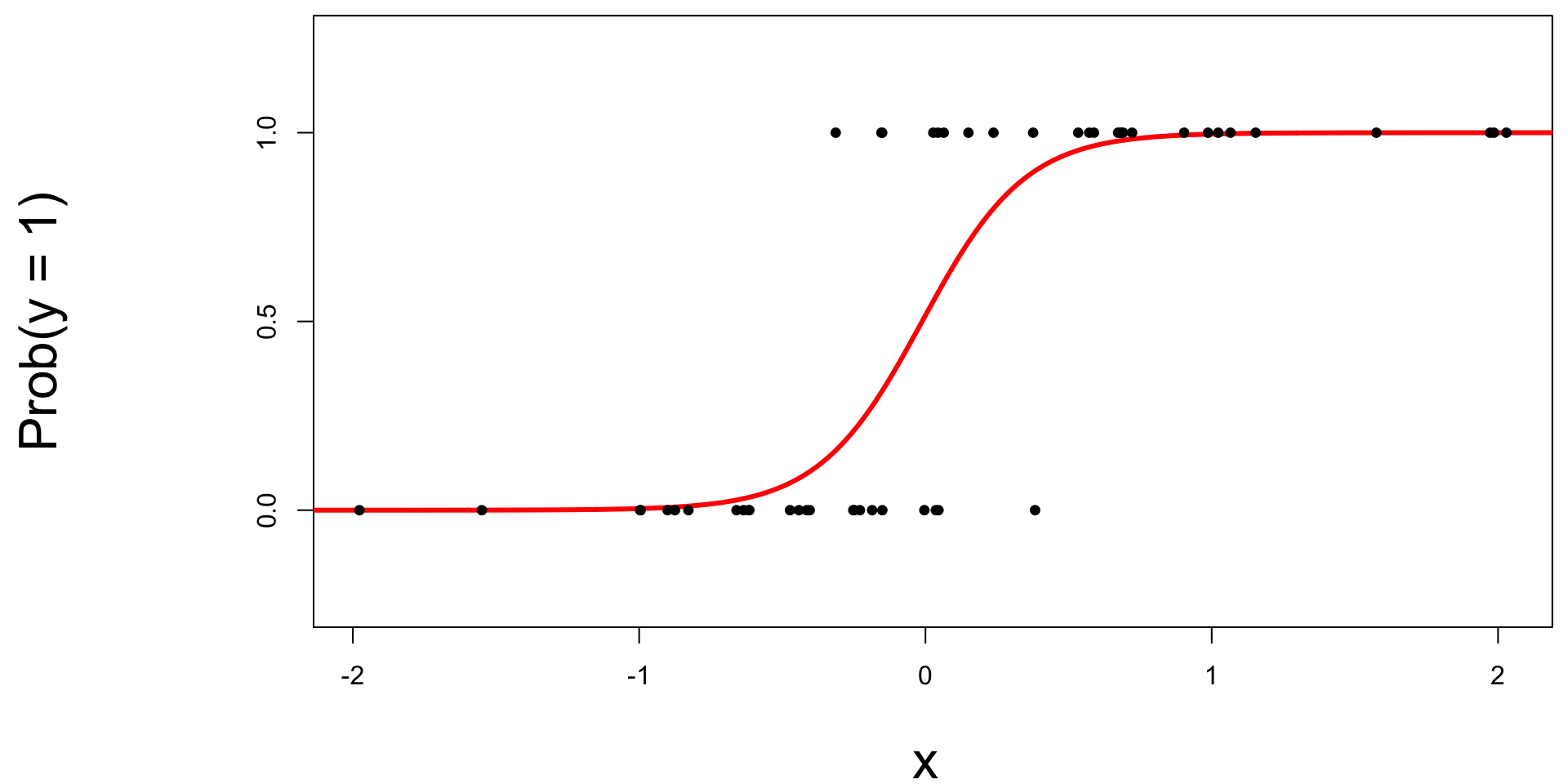
• if \(\text{Prob}(y=1)\leq p^*\), then predict \(\widehat{y}=0\);
• if \(\text{Prob}(y=1)> p^*\), then predict \(\widehat{y}=1\).

Step 1: pick a threshold

Select a number \(0 < p^* < 1\):

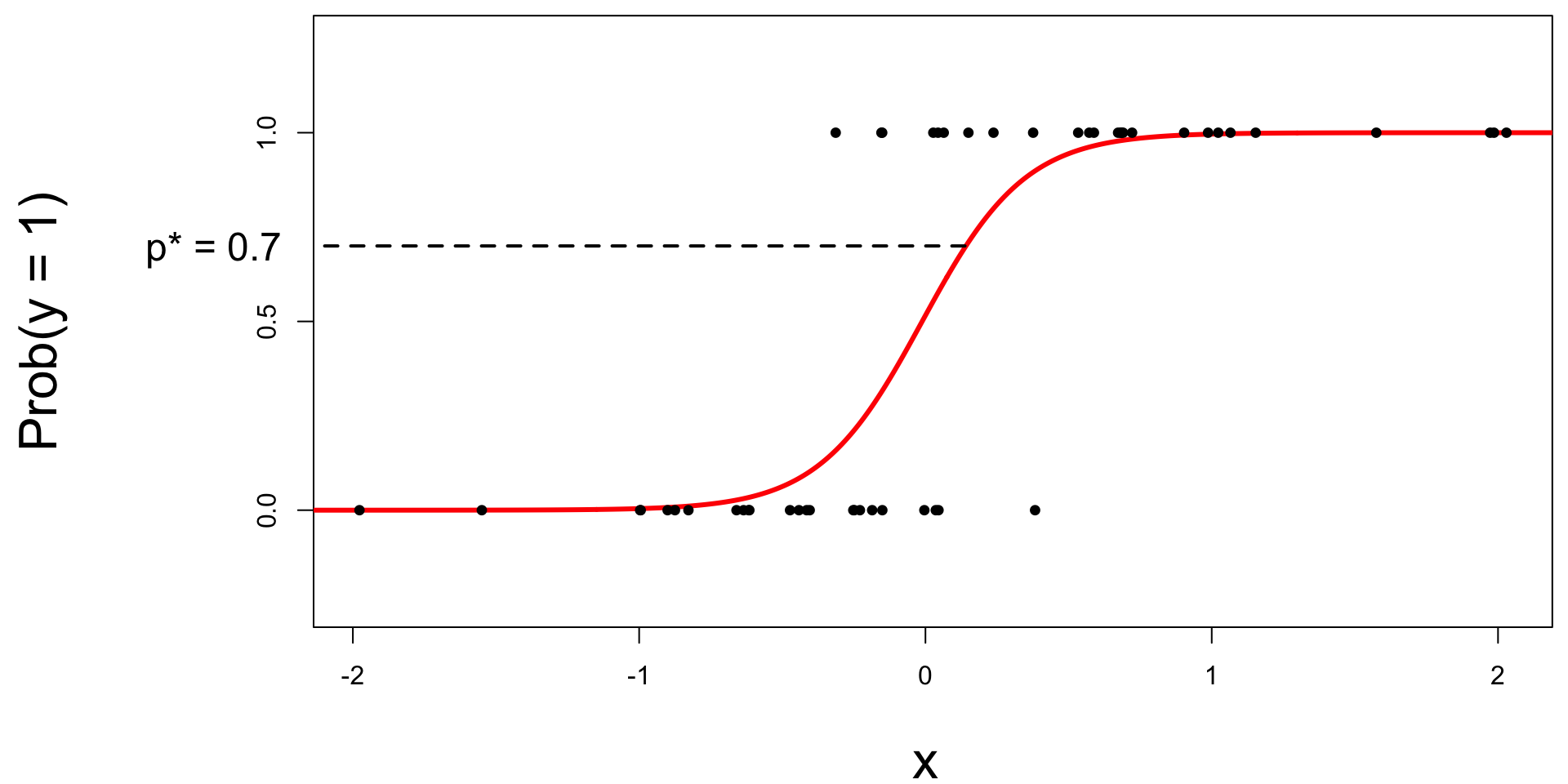
• if \(\text{Prob}(y=1)\leq p^*\), then predict \(\widehat{y}=0\);
• if \(\text{Prob}(y=1)> p^*\), then predict \(\widehat{y}=1\).

Step 2: find the “decision boundary”

Solve for the x-value that matches the threshold:

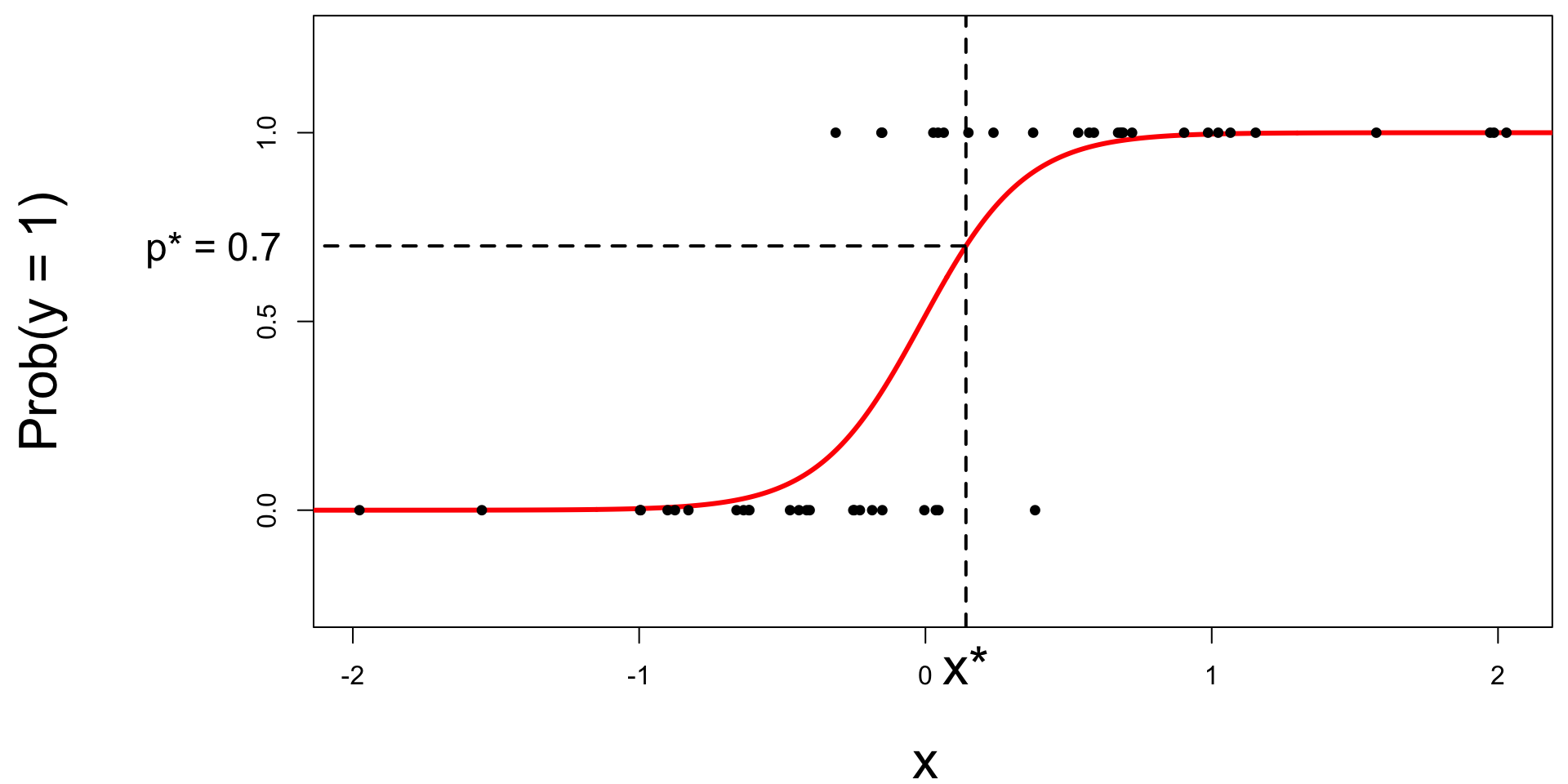
• if \(\text{Prob}(y=1)\leq p^*\), then predict \(\widehat{y}=0\);
• if \(\text{Prob}(y=1)> p^*\), then predict \(\widehat{y}=1\).

Step 3: classify a new arrival

A new person shows up with \(x_{\text{new}}\). Which side of the boundary are they on?

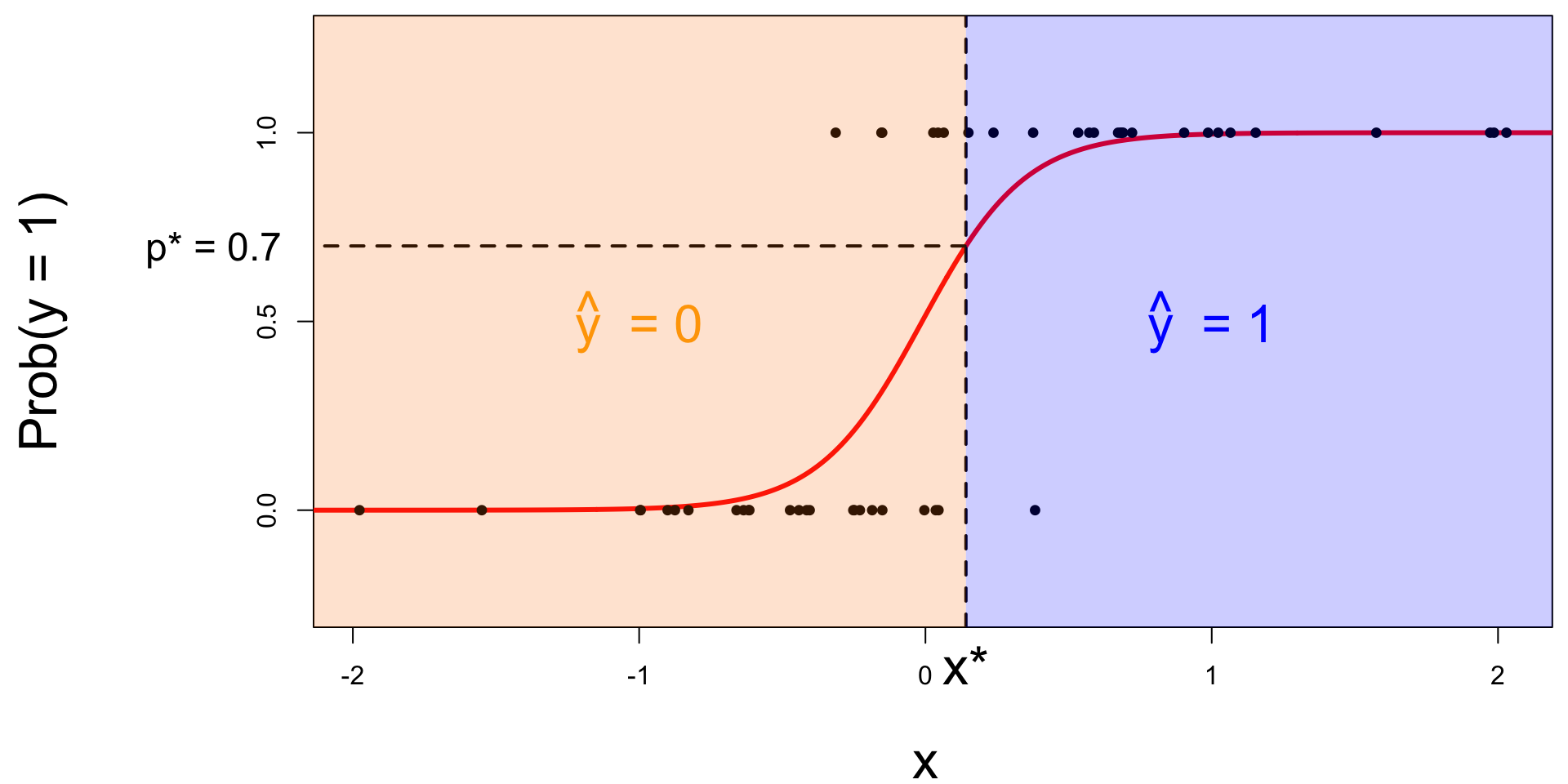
• if \(x_{\text{new}} \leq x^\star\), then \(\text{Prob}(y=1)\leq p^*\), so predict \(\widehat{y}=0\) for the new person;
• if \(x_{\text{new}} > x^\star\), then \(\text{Prob}(y=1)> p^*\), so predict \(\widehat{y}=1\) for the new person.

Let’s change the threshold

A new person shows up with \(x_{\text{new}}\). Which side of the boundary are they on?

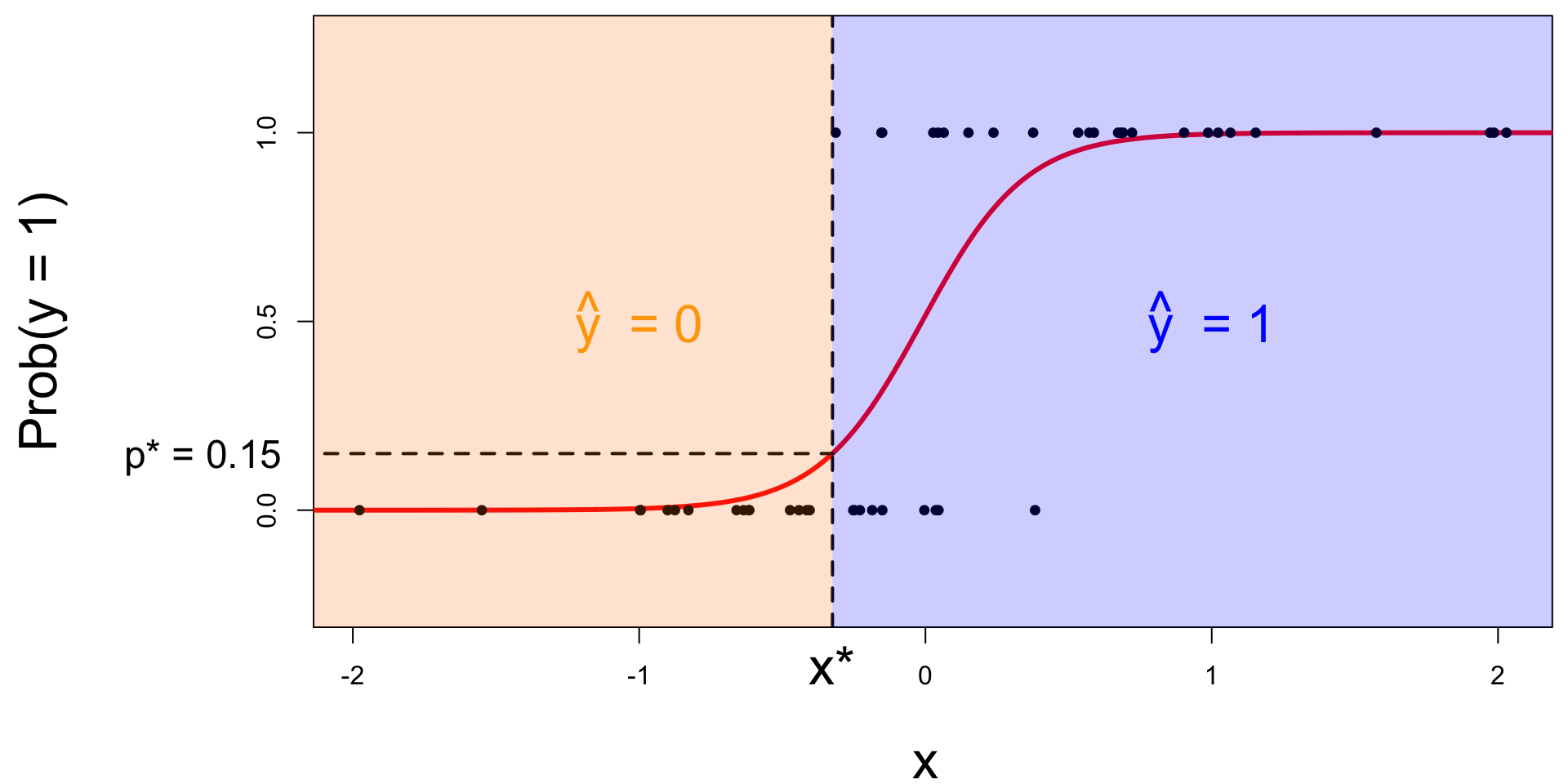
• if \(x_{\text{new}} \leq x^\star\), then \(\text{Prob}(y=1)\leq p^*\), so predict \(\widehat{y}=0\) for the new person;
• if \(x_{\text{new}} > x^\star\), then \(\text{Prob}(y=1)> p^*\), so predict \(\widehat{y}=1\) for the new person.

Let’s change the threshold

A new person shows up with \(x_{\text{new}}\). Which side of the boundary are they on?

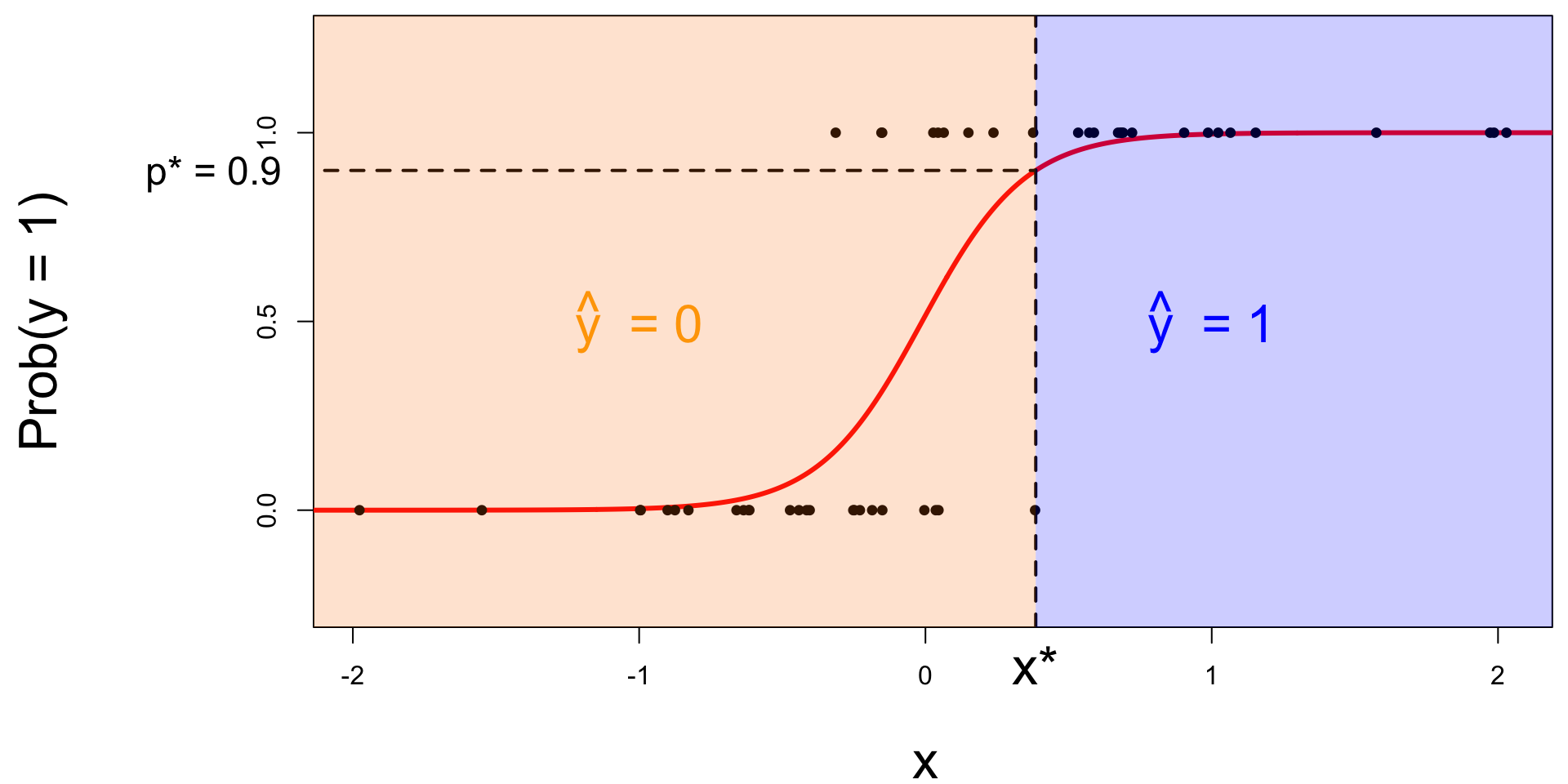
• if \(x_{\text{new}} \leq x^\star\), then \(\text{Prob}(y=1)\leq p^*\), so predict \(\widehat{y}=0\) for the new person;
• if \(x_{\text{new}} > x^\star\), then \(\text{Prob}(y=1)> p^*\), so predict \(\widehat{y}=1\) for the new person.

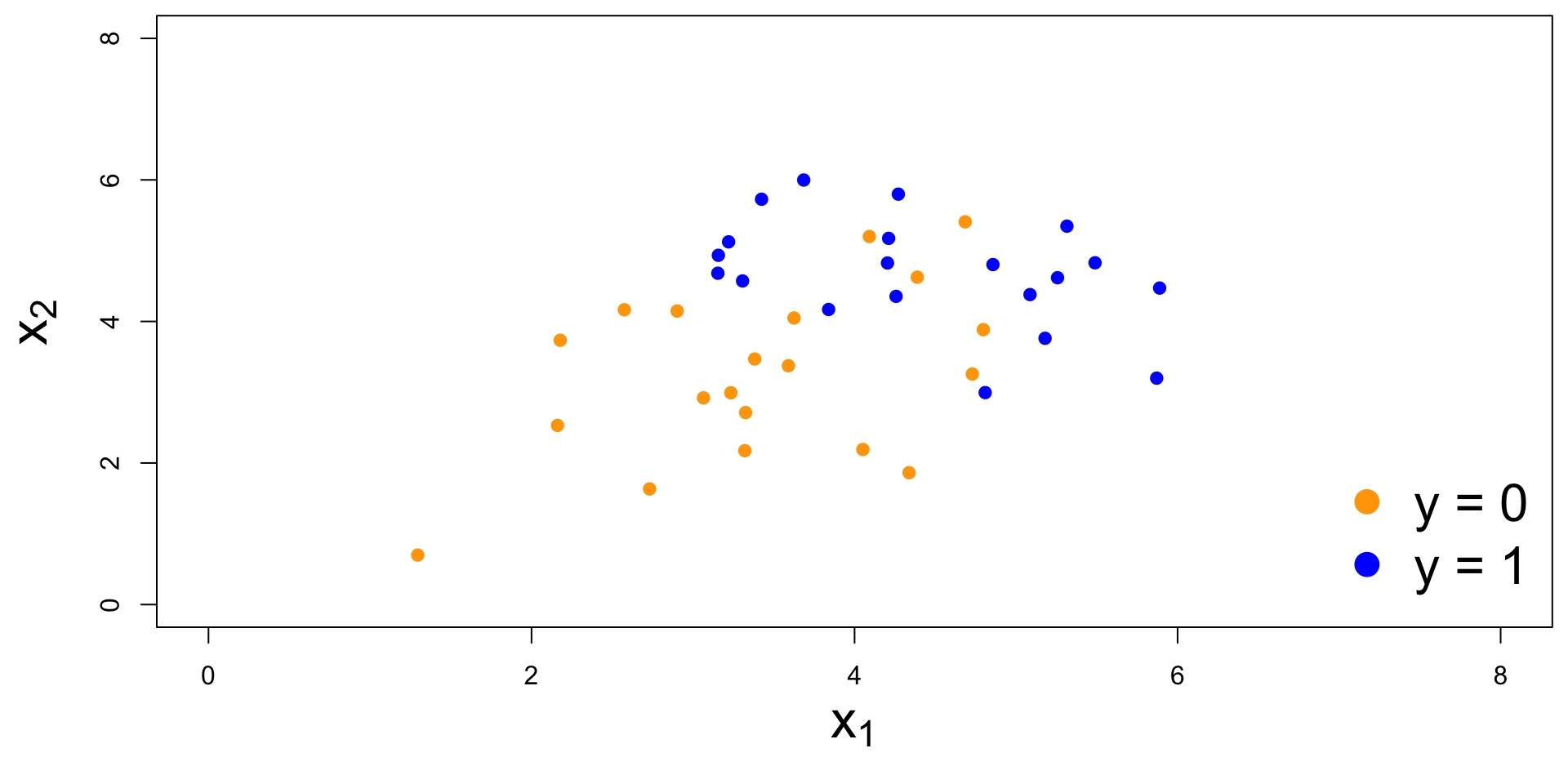
Nothing special about one predictor…

Two numerical predictors and one binary response:

“Multiple” logistic regression

On the probability scale:

\[ \text{Prob}(y = 1) = \frac{e^{\beta_0+\beta_1x_1+\beta_2x_2+...+\beta_mx_m}}{1+e^{\beta_0+\beta_1x_1+\beta_2x_2+...+\beta_mx_m}}. \]

For the log-odds, a multiple linear regression:

\[ \log\left(\frac{p}{1-p}\right) = \beta_0+\beta_1x_1+\beta_2x_2+...+\beta_mx_m. \]

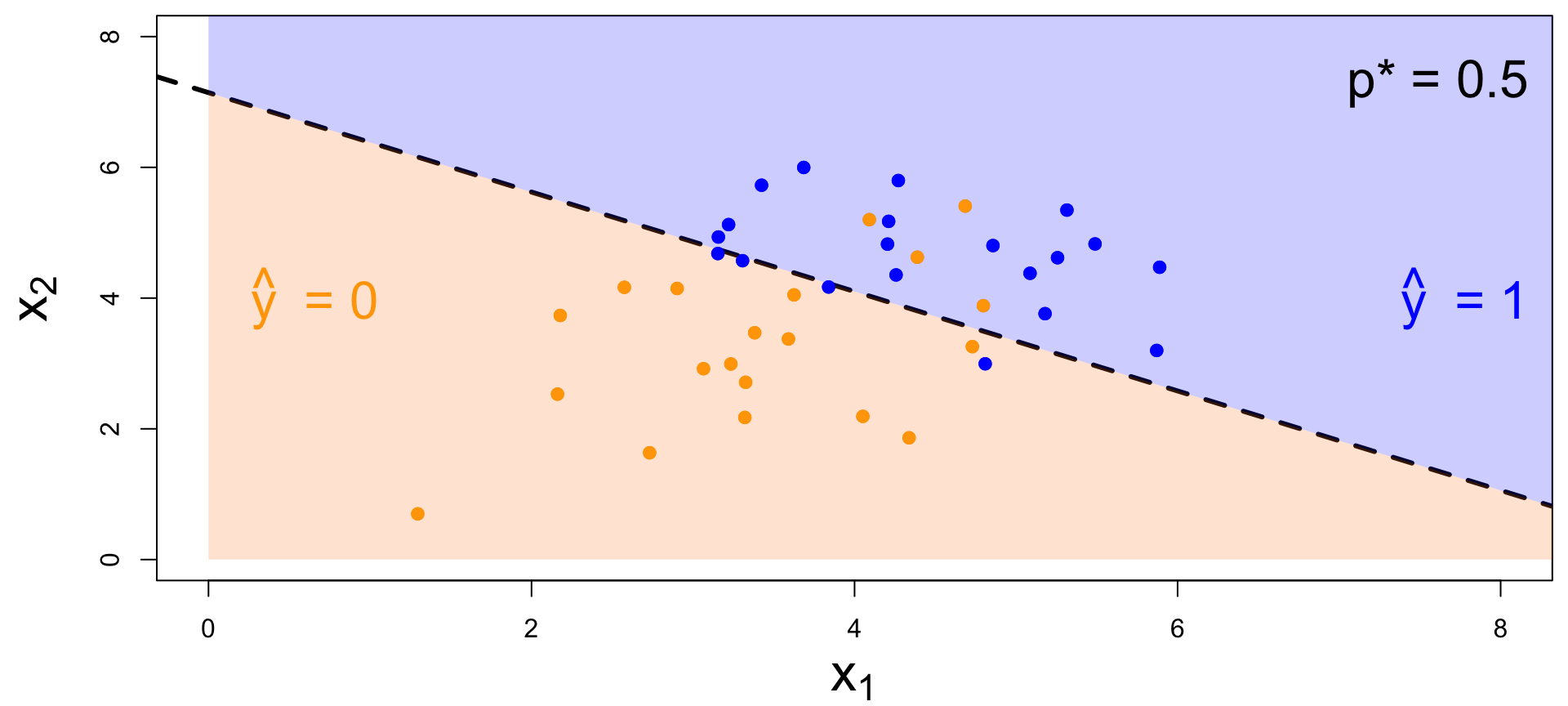
Decision boundary, again

It’s linear! Consider two numerical predictors:

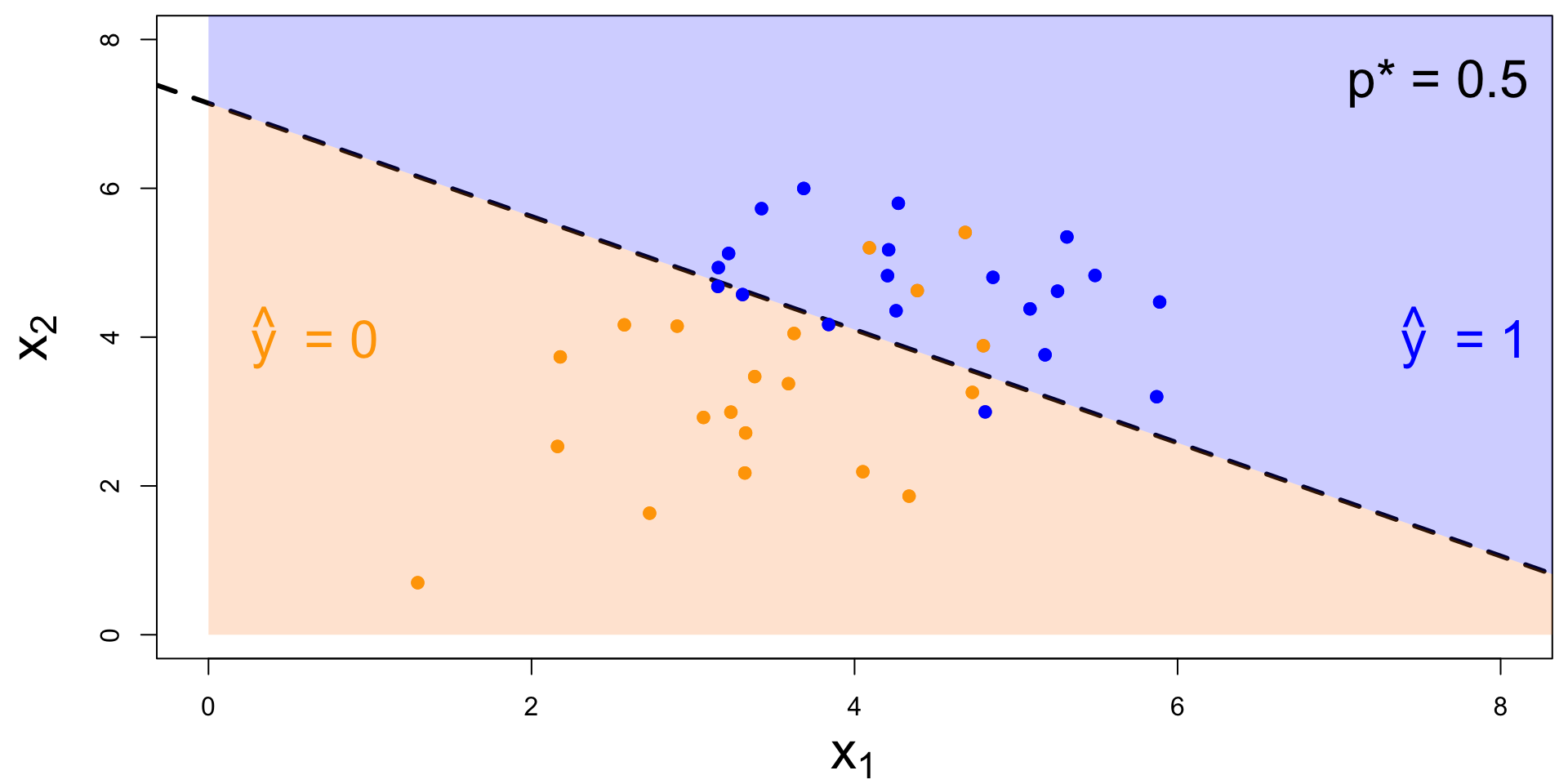
• if new \((x_1,\,x_2)\) below, \(\text{Prob}(y=1)\leq p^*\). Predict \(\widehat{y}=0\) for the new person;
• if new \((x_1,\,x_2)\) above, \(\text{Prob}(y=1)> p^*\). Predict \(\widehat{y}=1\) for the new person.

Decision boundary, again

It’s linear! Consider two numerical predictors:

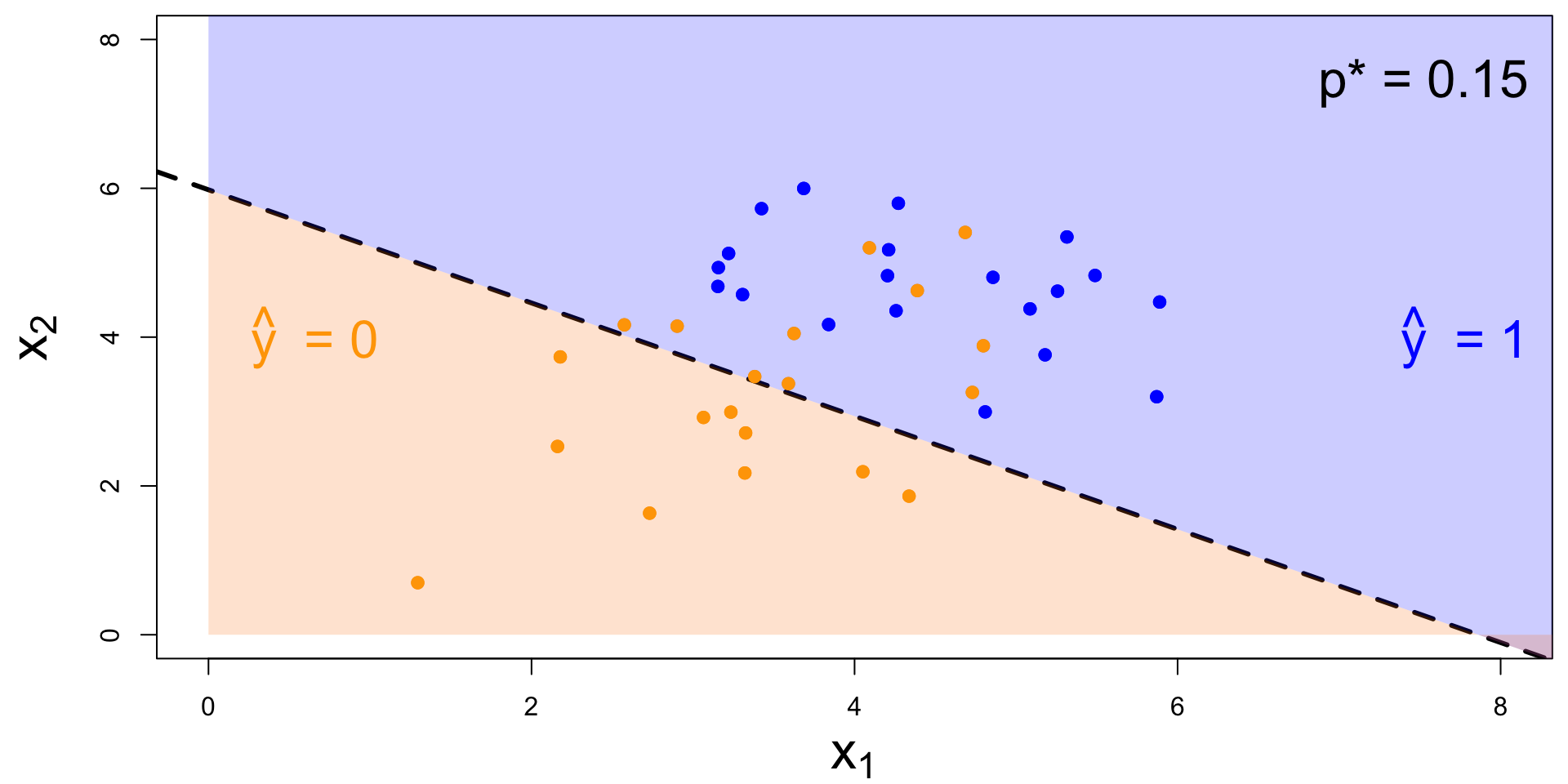
• if new \((x_1,\,x_2)\) below, \(\text{Prob}(y=1)\leq p^*\). Predict \(\widehat{y}=0\) for the new person;
• if new \((x_1,\,x_2)\) above, \(\text{Prob}(y=1)> p^*\). Predict \(\widehat{y}=1\) for the new person.

Decision boundary, again

It’s linear! Consider two numerical predictors:

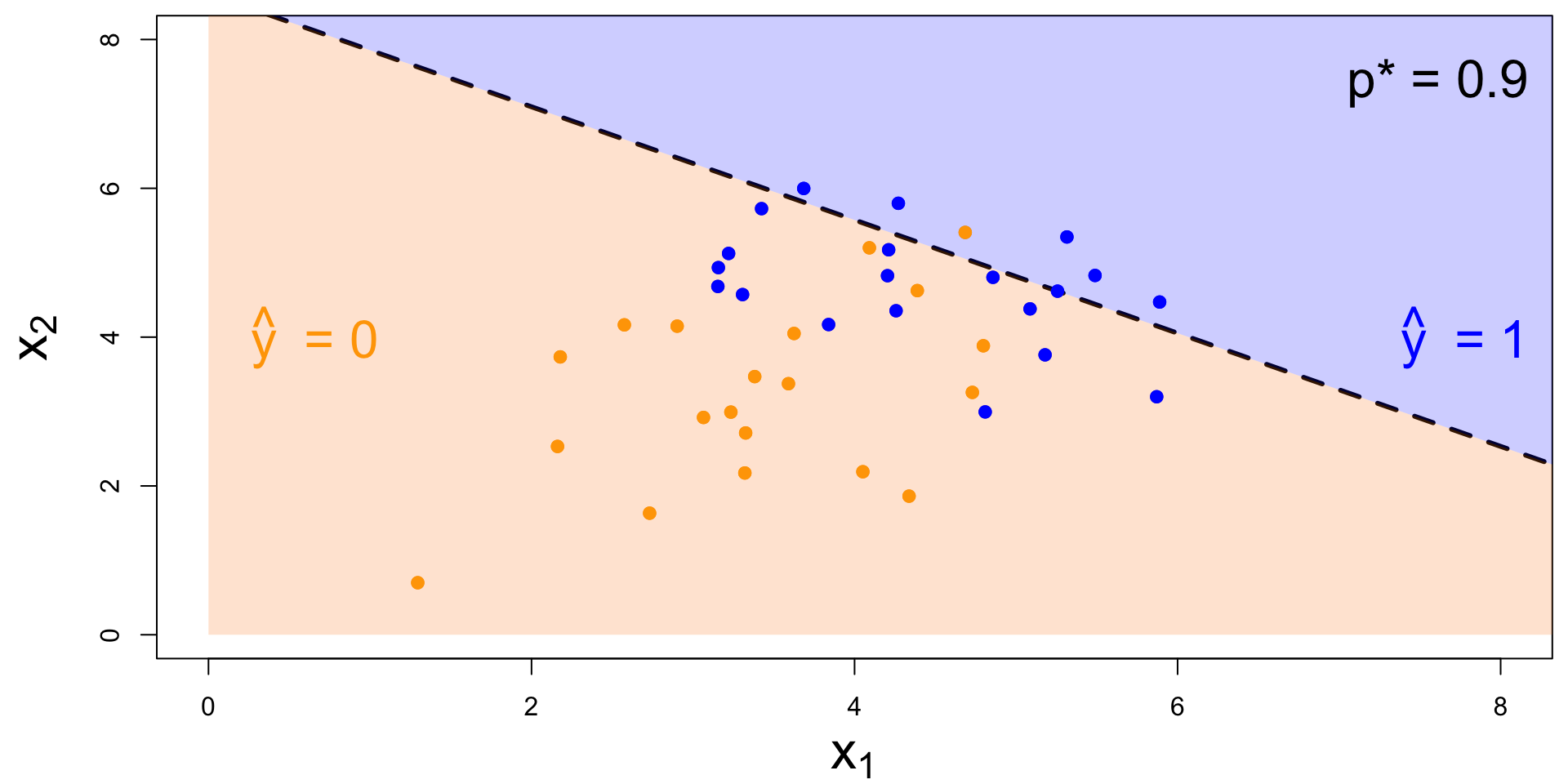
• if new \((x_1,\,x_2)\) below, \(\text{Prob}(y=1)\leq p^*\). Predict \(\widehat{y}=0\) for the new person;
• if new \((x_1,\,x_2)\) above, \(\text{Prob}(y=1)> p^*\). Predict \(\widehat{y}=1\) for the new person.

Note: the classifier isn’t perfect

• There are blue points in the orange region: spam (1) emails misclassified as legit (0);
• There are orange points in the blue region: legit (0) emails misclassified as spam (1).

How do you pick the threshold?

To balance out the two kinds of errors:

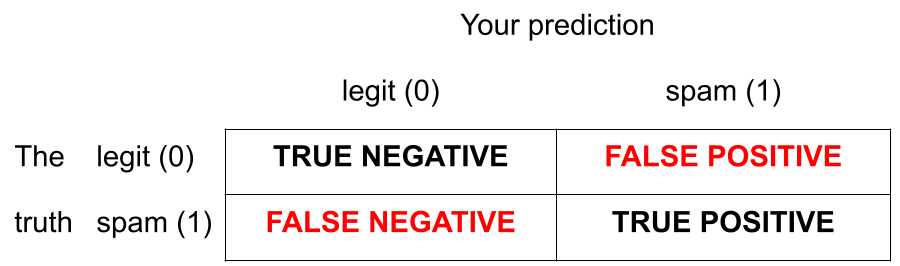
• High threshold >> Hard to classify as 1 >> FP less likely; FN more likely
• Low threshold >> Easy to classify as 1 >> FP more likely; FN less likely

Silly examples

• Set p* = 0

  • Classify every email as spam (1);
  • No false negatives, but a lot of false positives;

• Set p* = 1

  • Classify every email as legit (0);
  • No false positives, but a lot of false negatives.

You pick a threshold in between to strike a balance. The exact number depends on context.

ae-13-spam-filter

• Go to your ae project in RStudio.

• If you haven’t yet done so, make sure all of your changes up to this point are committed and pushed, i.e., there’s nothing left in your Git pane.

• If you haven’t yet done so, click Pull to get today’s application exercise file: ae-13-spam-filter.qmd.

• Work through the application exercise in class, and render, commit, and push your edits.