Statistical inference

Lecture 21

John Zito

Duke University
STA 199 Spring 2025

2025-04-08

While you wait…

Go to your ae project in RStudio.
Make sure all of your changes up to this point are committed and pushed, i.e., there’s nothing left in your Git pane.
Click Pull to get today’s application exercise file: ae-17-inference-practice.qmd.
Wait until you’re prompted to work on the application exercise during class before editing the file.

Recap: statistical inference

The population model (greek letters, no hats)

This is an idealized representation of the data: \[ y = \beta_0+\beta_1x +\varepsilon; \]
There is some “true line” floating out there with a “true slope” \(\beta_1\) and “true intercept” \(\beta_0\);
With infinite amounts of perfectly measured data, we could know \(\beta_0\) and \(\beta_1\) exactly;
We don’t have that, so we must use finite amounts of imperfect data to estimate;
We are especially interested in \(\beta_1\) because is characterizes the association between \(x\) and \(y\), which is useful for prediction.

“Three branches of statistical government”

\(\beta_1\) is an unknown quantity we are trying to learn about using noisy, imperfect data. Learning comes in three flavors:

POINT ESTIMATION: get a single-number best guess for \(\beta_1\);
INTERVAL ESTIMATION: get a range of likely values for \(\beta_1\) that characterizes (sampling) uncertainty;
HYPOTHESIS TESTING: use the data to distinguish competing claims about \(\beta_1\).

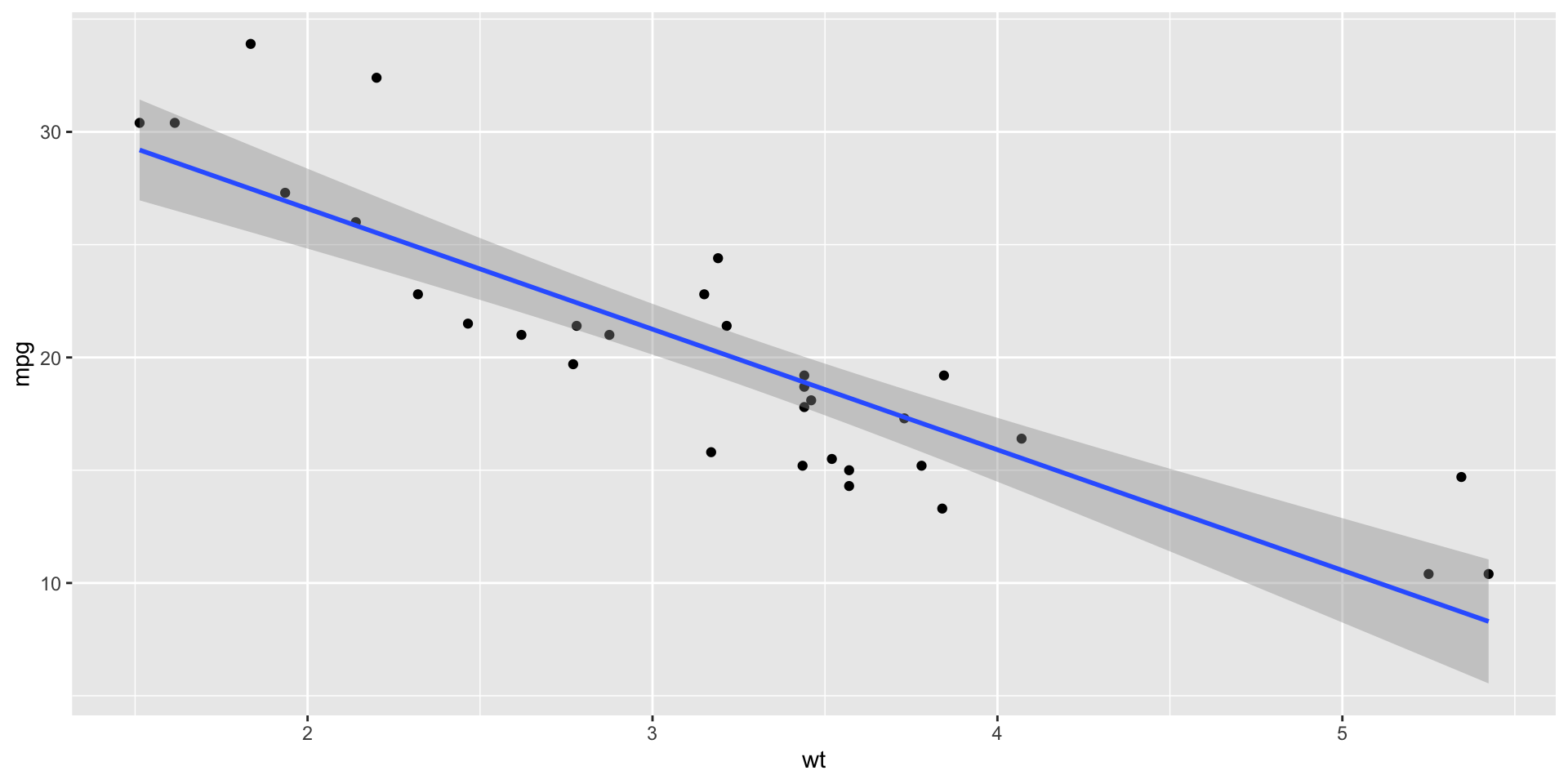
Point estimation (roman letters, hats!)

We estimate \(\beta_0\) and \(\beta_1\) with the coefficients of the best fit line:

\[ \hat{y}=b_0+b_1x. \]

“Best” means “least squares.” We pick the estimates so that the sum of squared residuals is as small as possible.

Point estimation

ggplot(mtcars, aes(x = wt, y = mpg)) + 
  geom_point() +
  geom_smooth(method = "lm")

Point estimation

linear_reg() |>
  fit(mpg ~ wt, data = mtcars) |>
  tidy()

# A tibble: 2 × 5
  term        estimate std.error statistic  p.value
  <chr>          <dbl>     <dbl>     <dbl>    <dbl>
1 (Intercept)    37.3      1.88      19.9  8.24e-19
2 wt             -5.34     0.559     -9.56 1.29e-10

Sampling uncertainty

How do our point estimates vary across alternative, hypothetical datasets?
- If they vary alot, uncertainty is high, and results are unreliable;
- if they vary only a little, uncertainty is low, and results are more reliable.
We can use the bootstrap to construct alternative datasets and assess the sensitivity of our estimates to changes in the data.

Bootstrap distribution

This histogram displays variation in the slope estimate across alternative datasets.

- Large spread >> high uncertainty;
- Small spread >> lower uncertainty.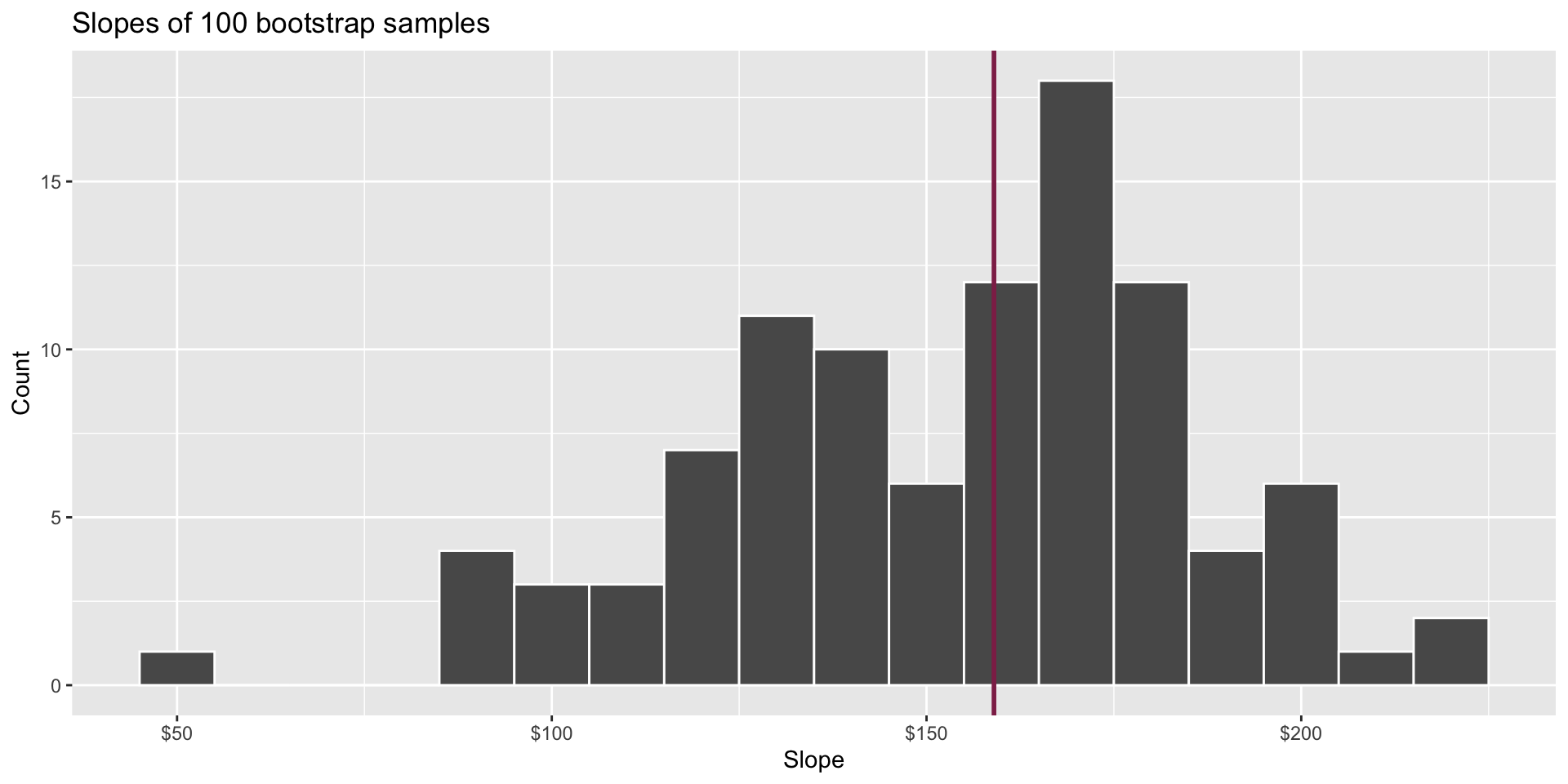

Confidence interval

Pick a range that swallows up a large % of the histogram:

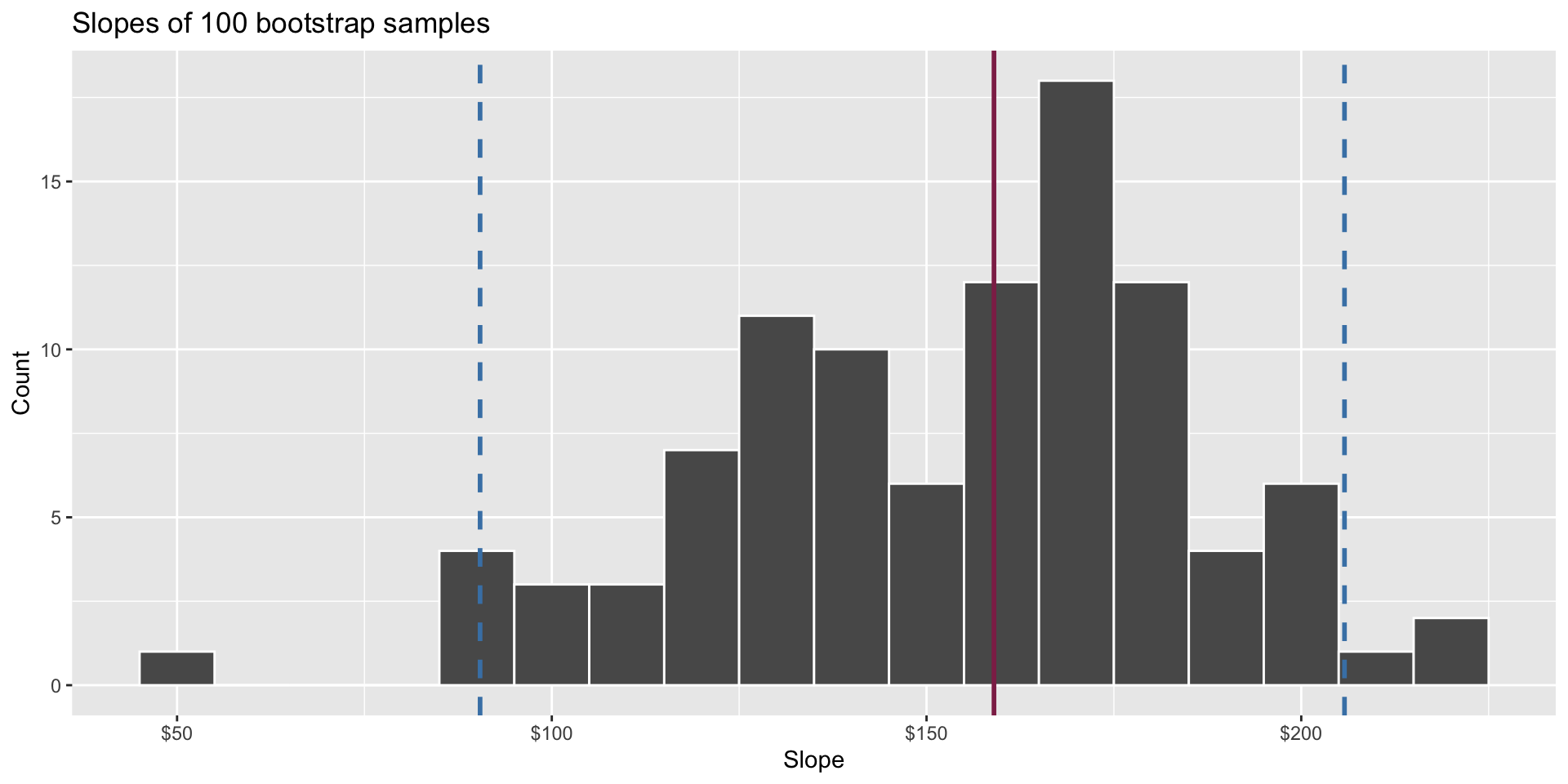
We use quantiles (think IQR) but there are other ways.

Hypothesis testing

Two competing claims about \(\beta_1\): \[ \begin{aligned} H_0&: \beta_1=0\quad(\text{nothing going on})\\ H_A&: \beta_1\neq0\quad(\text{something going on}) \end{aligned} \]
Do the data strongly favor one or the other?
How can we quantify this?

Hypothesis testing

Think hypothetically: if the null hypothesis were in fact true, would my results be out of the ordinary?
- if no, then the null could be true;
- if yes, then the null might be bogus;
My results represent the reality of actual data. If they conflict with the null, then you throw out the null and stick with reality;
How do we quantify “would my results be out of the ordinary”?

Null distribution

If the null happened to be true, how would we expect our results to vary across datasets? We can use simulation to answer this:

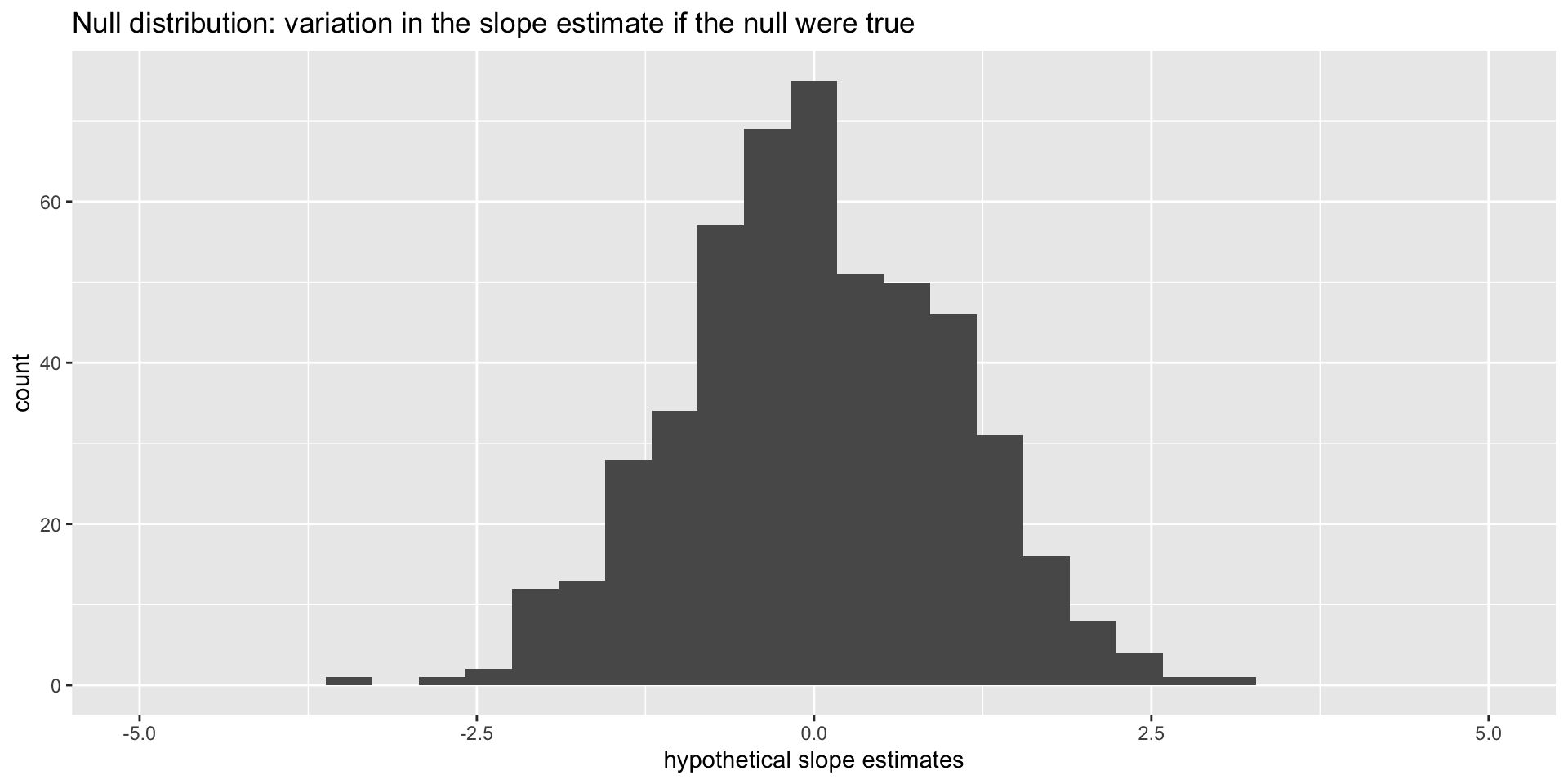
This is how the world should look if the null is true.

Null distribution versus reality

Locate the actual results of your actual data analysis under the null distribution. Are they in the middle? Are they in the tails?

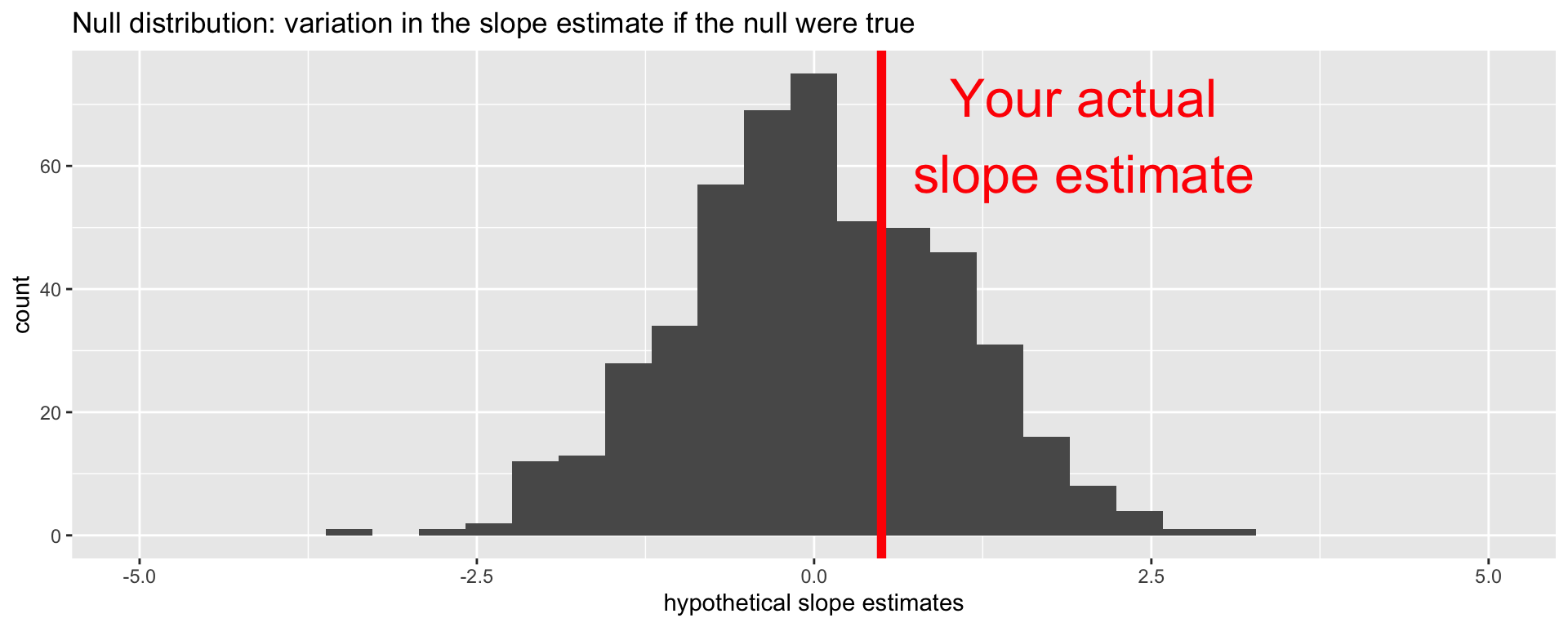
Are these results in harmony or conflict with the null?

Null distribution versus reality

Locate the actual results of your actual data analysis under the null distribution. Are they in the middle? Are they in the tails?

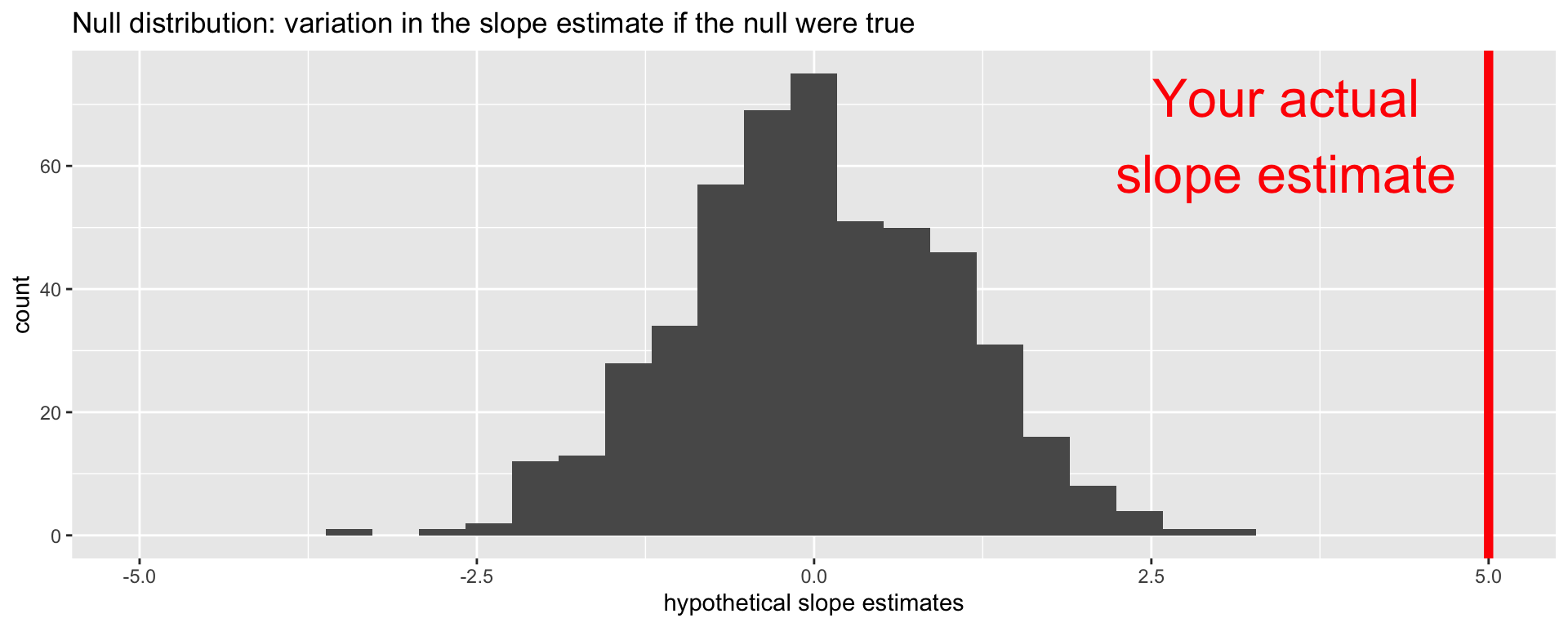
Are these results in harmony or conflict with the null?

Null distribution versus reality

Locate the actual results of your actual data analysis under the null distribution. Are they in the middle? Are they in the tails?

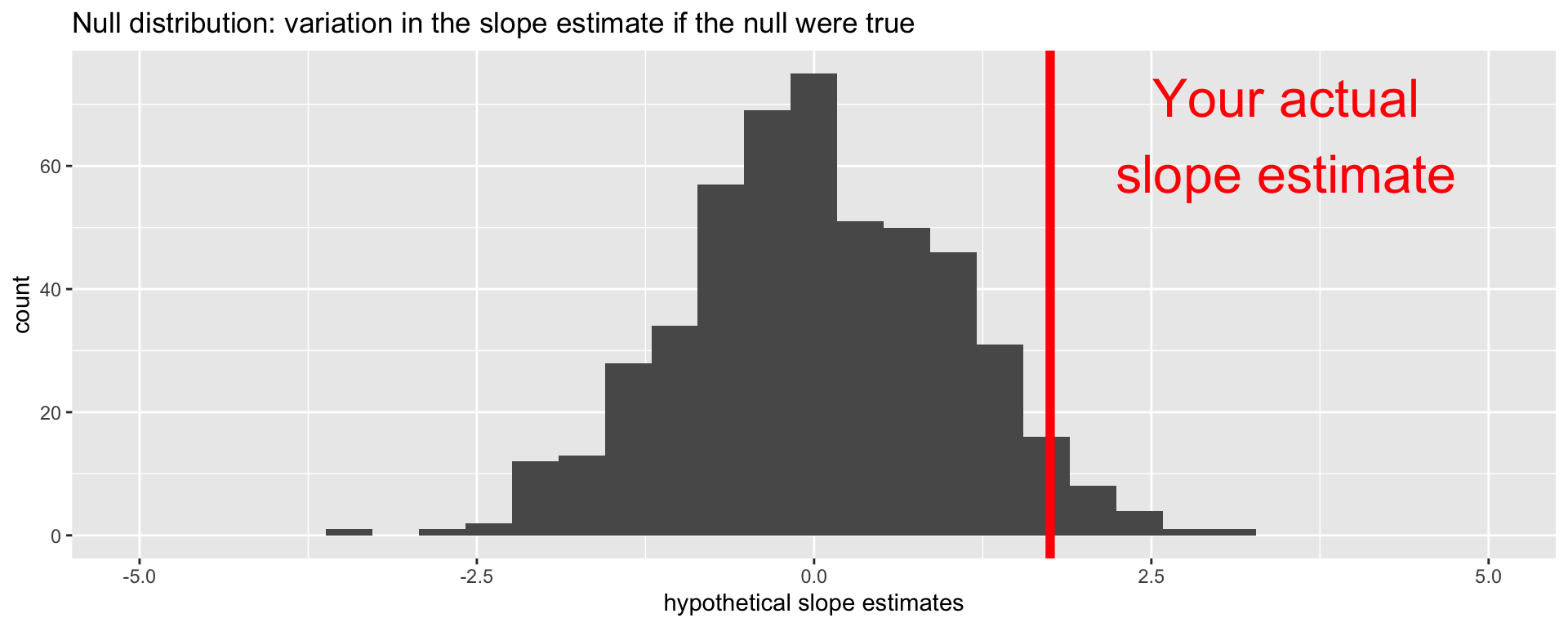
Are these results in harmony or conflict with the null?

p-value

The \(p\)-value is the probability of being even farther out in the tails of the null distribution than your results already were.

if this number is very low, then your results would be out of the ordinary if the null were true, so maybe the null was never true to begin with;
if this number is high, then your results may be perfectly compatible with the null.

p-value

p-value is the fraction of the histogram area shaded red:

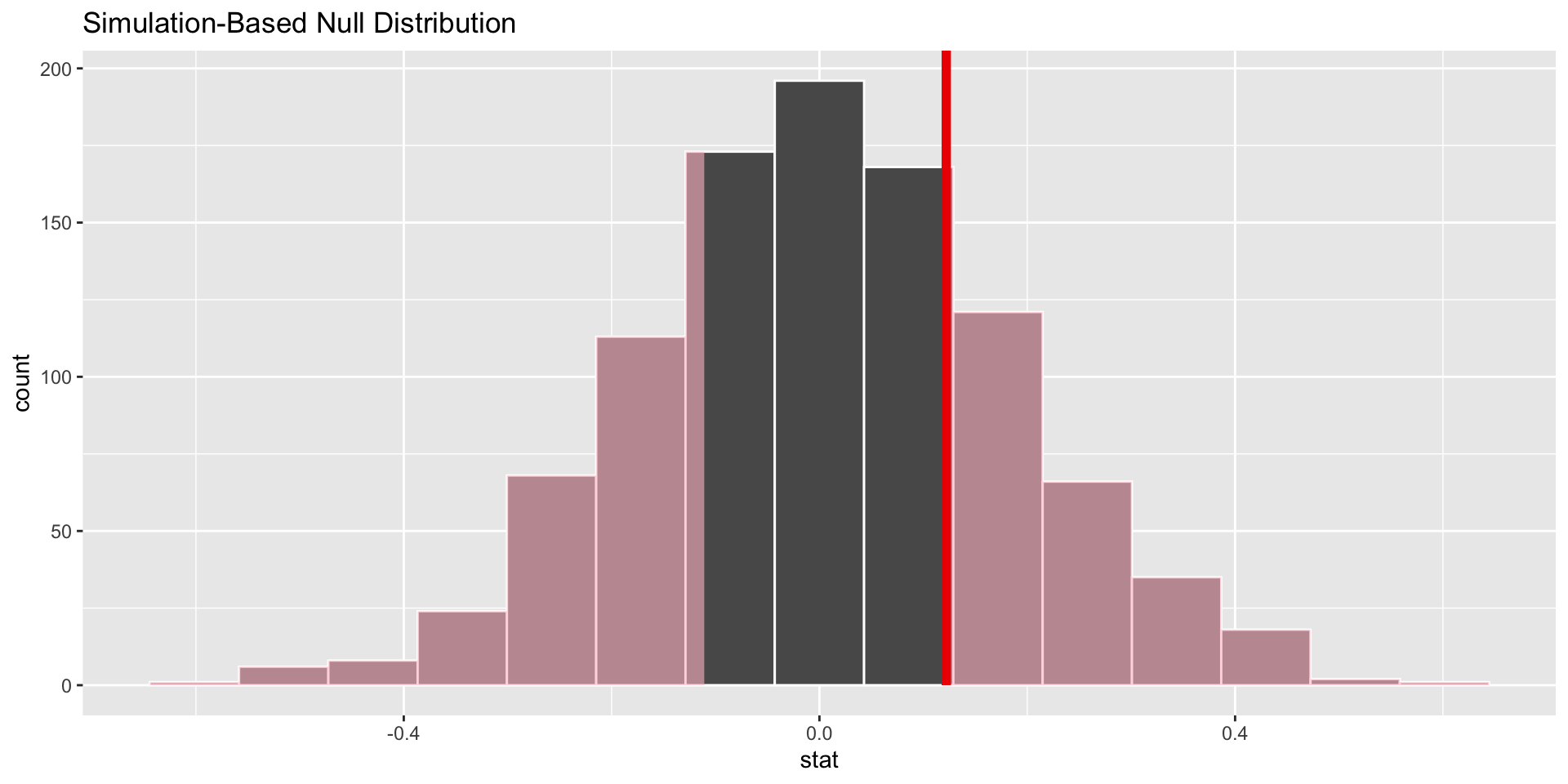
Big ol’ p-value. Null looks plausible

p-value

p-value is the fraction of the histogram area shaded red:

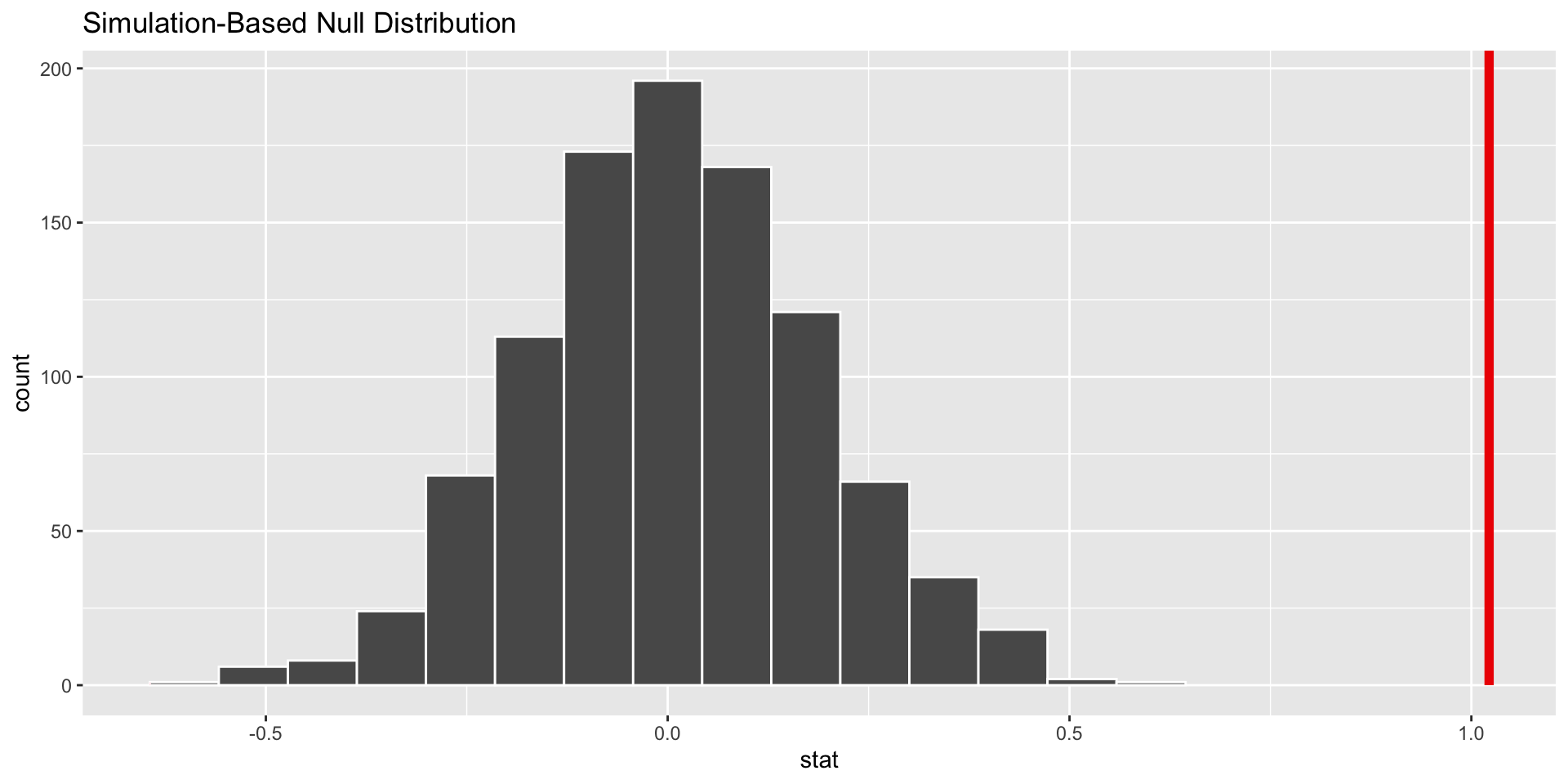
p-value is basically zero. Null looks bogus.

p-value

p-value is the fraction of the histogram area shaded red:

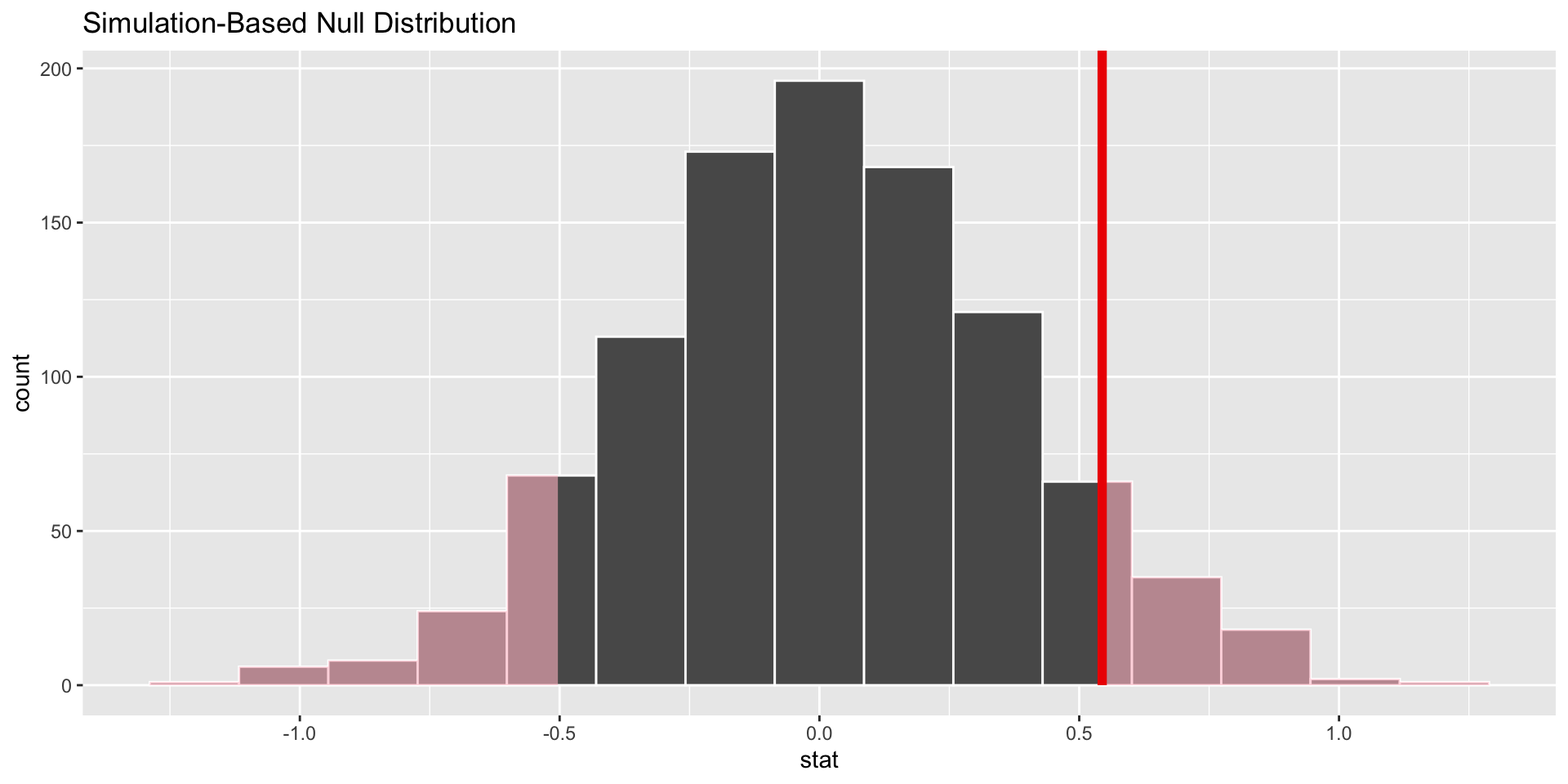
p-value is…kinda small? Null looks…?

Discernibility level

How do we decide if the p-value is big enough or small enough?
Pick a threshold \(\alpha\in[0,\,1]\) called the discernibility level:
- If \(p\text{-value} < \alpha\), reject null and accept alternative;
- If \(p\text{-value} \geq \alpha\), fail to reject null;
Standard choices: \(\alpha=0.01, 0.05, 0.1, 0.15\).

Pop quiz! (not really)

Take a moment to complete this ungraded check-in about statistical inference:

https://canvas.duke.edu/courses/50057/quizzes/33637

(It’s also linked on the course homepage)

What is \(b_1\)?

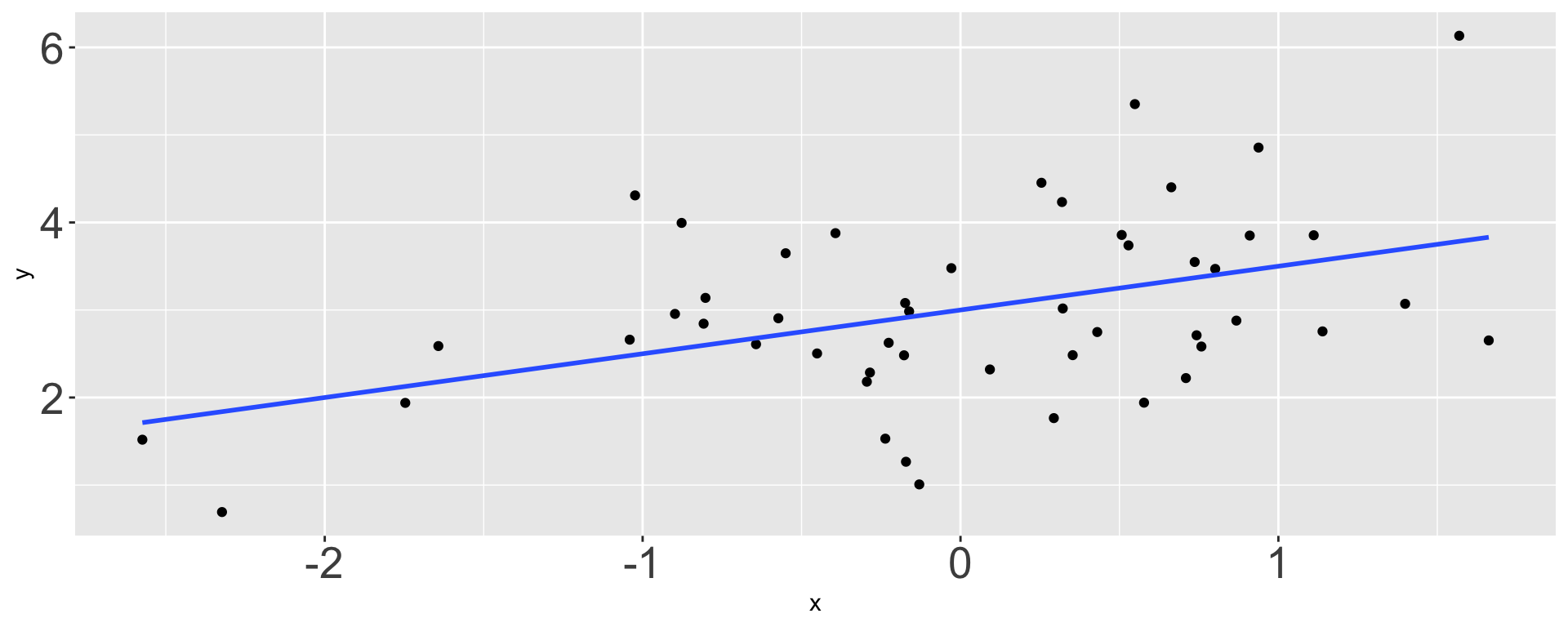
-1 / 2
0
1 / 4

1 / 2 (correct)
1
2

What is \(b_0\)?

1
1.75

2
3 (correct)

Which of these could be a bootstrap sample?

This is the original dataset:

Rows: 5
Columns: 1
$ scores <dbl> 1.563, -0.515, 1.206, -0.411, 0.523

A (correct)	B	C	D
-0.515	1.563	-0.515	-0.522
-0.411	-0.411	-0.411	1.12
1.563	-0.515	-0.411	1.206
-0.515		1.563	0.68
-0.515		1.563	0.83
		0.523
		1.563

Which is a 98% confidence interval?

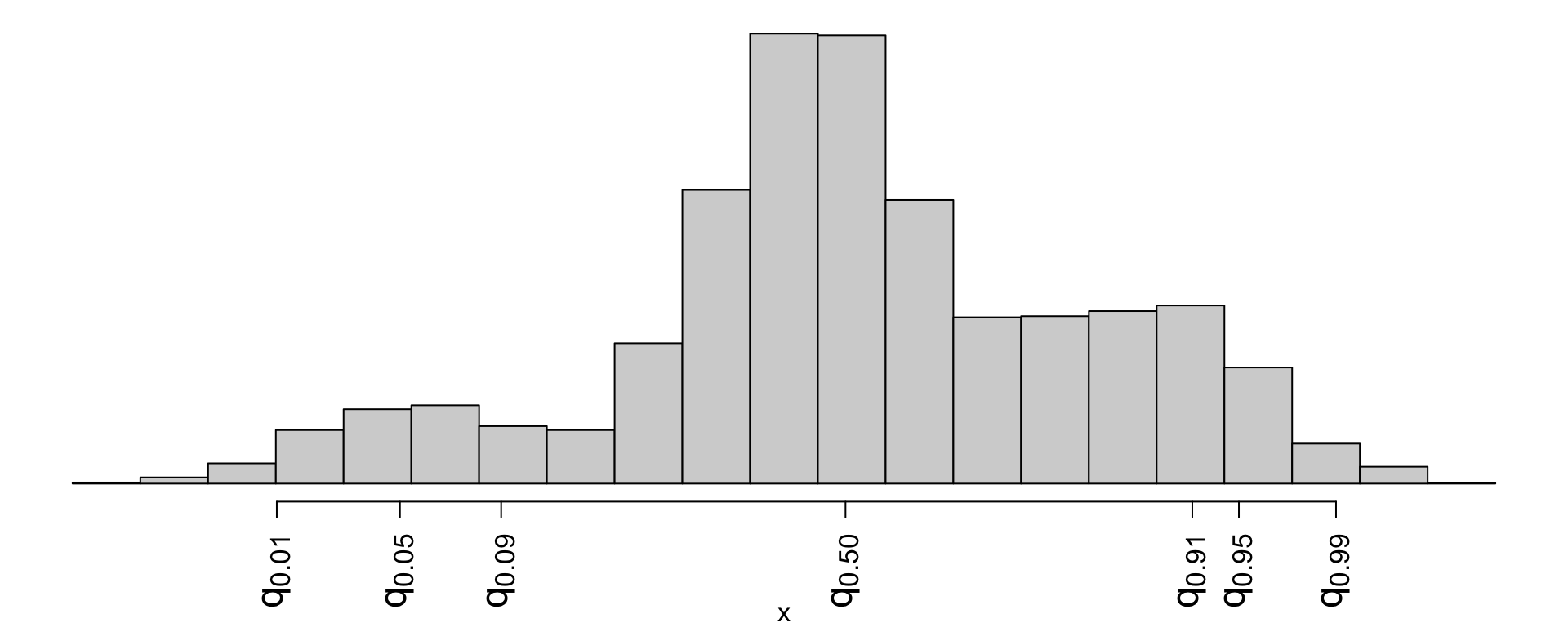
\((q_{0.01},\,q_{0.91})\)
\((q_{0.01},\,q_{0.99})\) (correct)

\((q_{0.09},\,q_{0.95})\)
\((q_{0.05},\,q_{0.99})\)

Match the picture to the p-value.

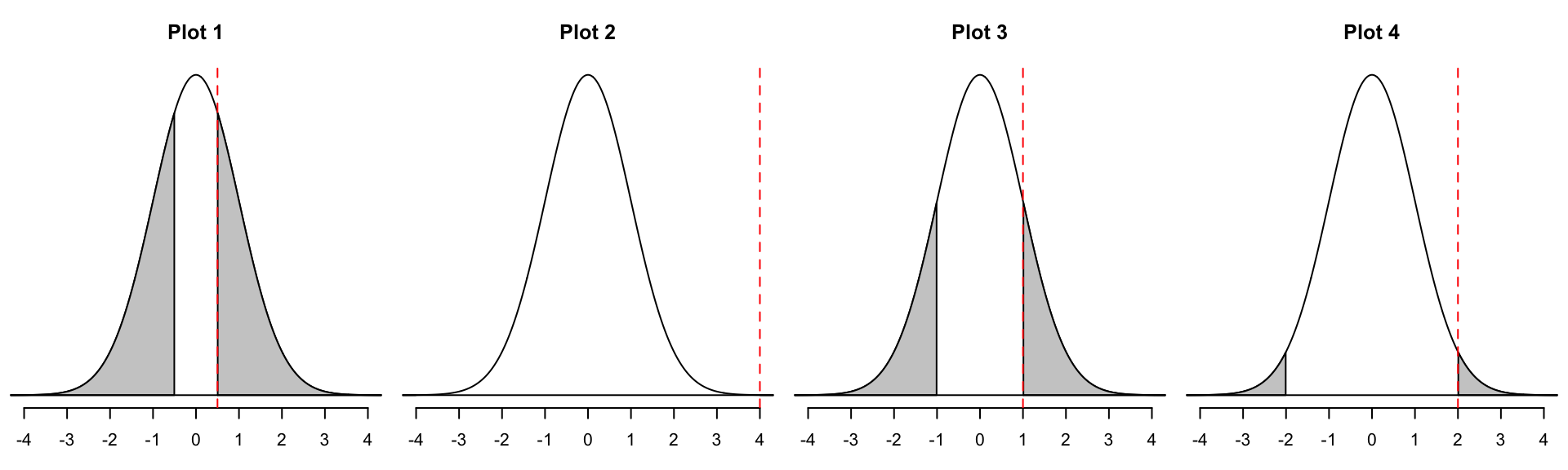
0 (Plot 2)
0.045 (Plot 4)

0.32 (Plot 3)
0.62 (Plot 1)

Which could be the null distribution of the test?

For these hypotheses

\[ \begin{aligned} H_0&: \beta_1=5\\ H_A&: \beta_1\neq 5. \end{aligned} \]

Answer: A

Application exercise

ae-17-inference-practice

Go to your ae project in RStudio.
If you haven’t yet done so, make sure all of your changes up to this point are committed and pushed, i.e., there’s nothing left in your Git pane.
If you haven’t yet done so, click Pull to get today’s application exercise file: ae-17-inference-practice.qmd.
Work through the application exercise in class, and render, commit, and push your edits.