AE 13: building a spam filter

Application exercise

In this application exercise, we will

Use logistic regression to fit a model for a binary response variable
Fit a logistic regression model in R
Use a logistic regression model for classification

To illustrate logistic regression, we will build a spam filter from email data.

The data come from incoming emails in David Diez’s (one of the authors of OpenIntro textbooks) Gmail account for the first three months of 2012. All personally identifiable information has been removed.

library(tidyverse)
library(tidymodels)
library(openintro)

glimpse(email)

Rows: 3,921
Columns: 21
$ spam         <fct> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, …
$ to_multiple  <fct> 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, …
$ from         <fct> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, …
$ cc           <int> 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 1, 2, 1, 0, 2, 0, …
$ sent_email   <fct> 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 1, 0, 0, 1, 0, 1, 0, 0, 1, …
$ time         <dttm> 2012-01-01 01:16:41, 2012-01-01 02:03:59, 2012-01-01 11:…
$ image        <dbl> 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, …
$ attach       <dbl> 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, …
$ dollar       <dbl> 0, 0, 4, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 2, 0, 5, 0, 0, …
$ winner       <fct> no, no, no, no, no, no, no, no, no, no, no, no, no, no, n…
$ inherit      <dbl> 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, …
$ viagra       <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, …
$ password     <dbl> 0, 0, 0, 0, 2, 2, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, …
$ num_char     <dbl> 11.370, 10.504, 7.773, 13.256, 1.231, 1.091, 4.837, 7.421…
$ line_breaks  <int> 202, 202, 192, 255, 29, 25, 193, 237, 69, 68, 25, 79, 191…
$ format       <fct> 1, 1, 1, 1, 0, 0, 1, 1, 0, 1, 1, 0, 1, 1, 1, 1, 1, 1, 0, …
$ re_subj      <fct> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1, 1, 1, 0, 1, 1, …
$ exclaim_subj <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, …
$ urgent_subj  <fct> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, …
$ exclaim_mess <dbl> 0, 1, 6, 48, 1, 1, 1, 18, 1, 0, 2, 1, 0, 10, 4, 10, 20, 0…
$ number       <fct> big, small, small, small, none, none, big, small, small, …

The variables we’ll use in this analysis are

spam: 1 if the email is spam, 0 otherwise
exclaim_mess: The number of exclamation points in the email message

Goal: Use the number of exclamation points in an email to predict whether or not it is spam.

Exercises

Exercise 1

Let’s start with some exploratory analysis:

Create a density plot to investigate the relationship between spam and exclaim_mess.

ggplot(email, aes(x = exclaim_mess, fill = spam)) + 
  geom_density()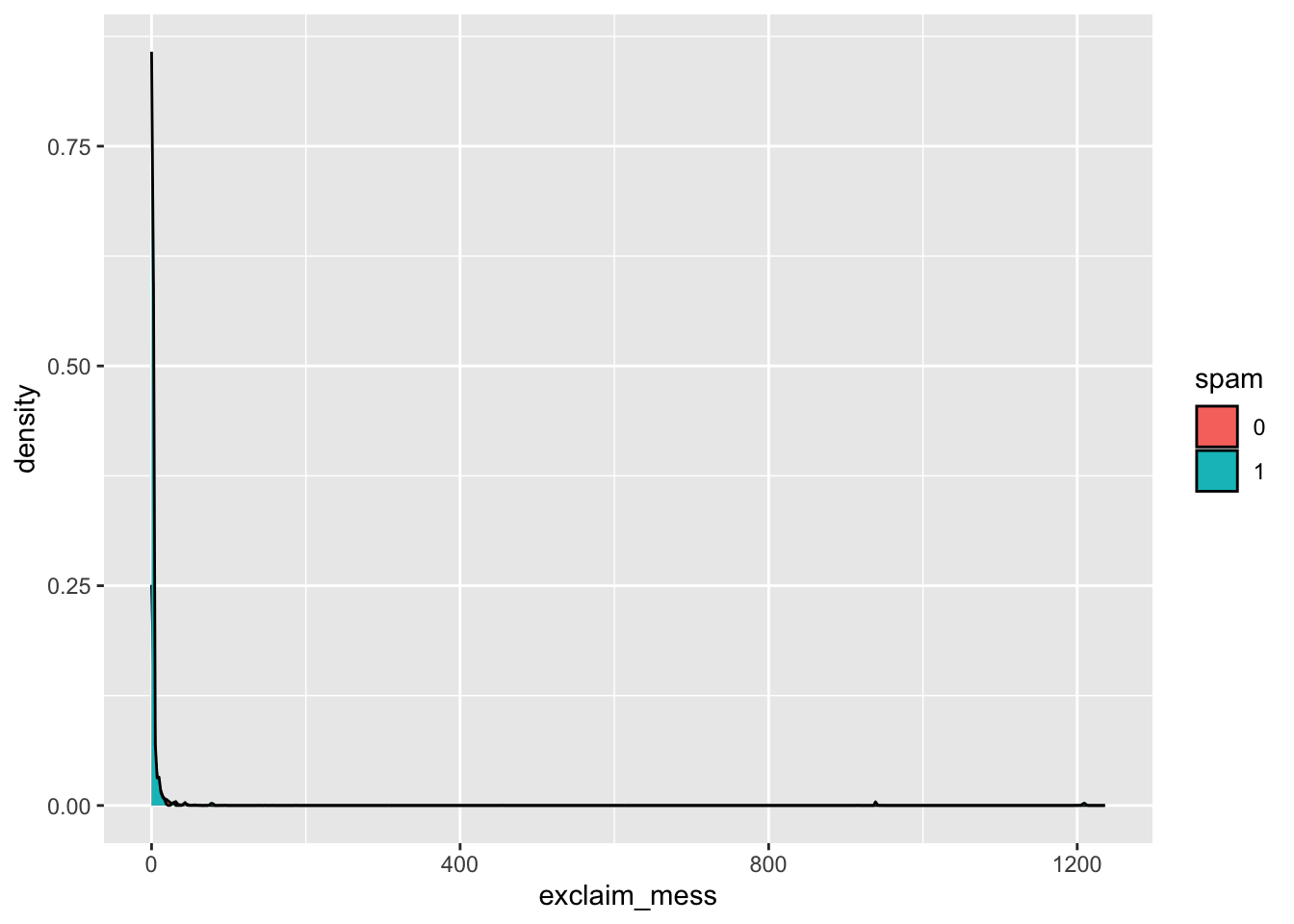

Additionally, calculate the mean number of exclamation points for both spam and non-spam emails.

email |>
  group_by(spam) |>
  summarize(mean_ep = mean(exclaim_mess))

# A tibble: 2 × 2
  spam  mean_ep
  <fct>   <dbl>
1 0        6.51
2 1        7.32

Exericse 2

Visualize a linear model fit for these data:

ggplot(email, aes(x = exclaim_mess, y = as.numeric(spam) - 1)) + 
  geom_point() + 
  geom_smooth(method = "lm") +
  labs(
    x = "# of exclamation marks in email",
    y = "e-mail type"
  ) +
  scale_y_continuous(breaks = c(0, 1),
                   labels = c("legit (0)", "spam (1)"))

`geom_smooth()` using formula = 'y ~ x'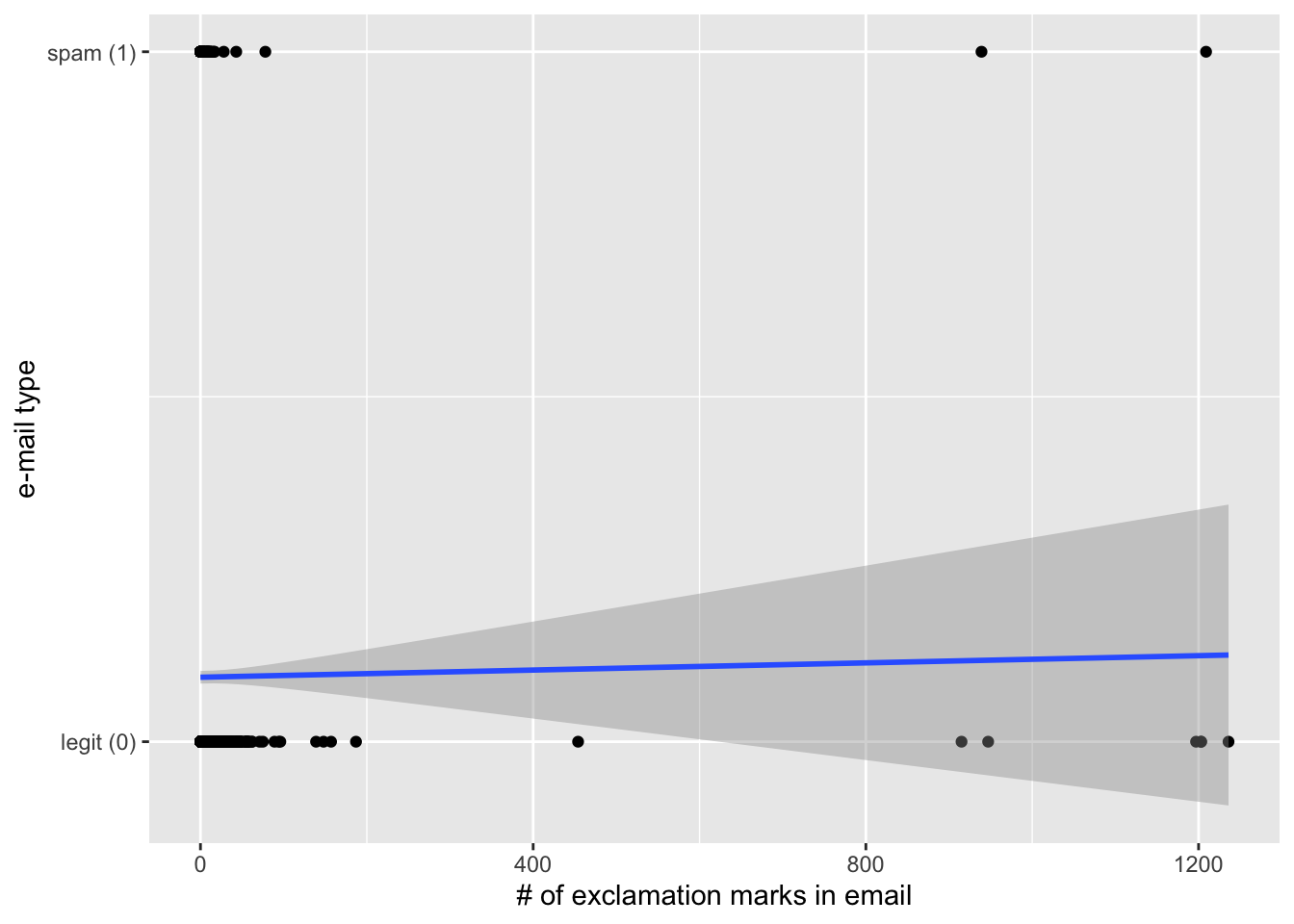

Is the linear model a good fit for the data? Why or why not?

Ans: Heavens no.

Exercise 3

Fit the logistic regression model using the number of exclamation points to predict the probability an email is spam:

log_fit <- logistic_reg() |>
  fit(spam ~ exclaim_mess, data = email)

tidy(log_fit)

# A tibble: 2 × 5
  term          estimate std.error statistic p.value
  <chr>            <dbl>     <dbl>     <dbl>   <dbl>
1 (Intercept)  -2.27      0.0553     -41.1     0    
2 exclaim_mess  0.000272  0.000949     0.287   0.774

Add your estimates to the fitted equation below

\[\log\Big(\frac{\hat{p}}{1-\hat{p}}\Big) = -2.27 + 0.00027 \times exclaim\_mess\]

How does the code above differ from previous code we’ve used to fit regression models?

Ans: linear_reg is changed to logistic_reg. Things are otherwise unchanged.

Exercise 4

What is the probability the email is spam if it contains 10 exclamation points? Answer the question using the predict() function.

new_email <- tibble(
  exclaim_mess = 10
  )

predict(log_fit, new_data = new_email, type = "prob")

# A tibble: 1 × 2
  .pred_0 .pred_1
    <dbl>   <dbl>
1   0.906  0.0937

A probability is nice, but we want an actual decision. Classify the darn email.

predict(log_fit, new_data = new_email, type = "class")

# A tibble: 1 × 1
  .pred_class
  <fct>      
1 0

The default behavior is to threshold the probabilities by 0.5.

Exercise 5

Fit a model with all variables in the dataset as predictors.

log_fit2 <- logistic_reg() |>
  fit(spam ~ ., data = email)

Warning: glm.fit: fitted probabilities numerically 0 or 1 occurred

If you used this model to classify the emails in the dataset, how would it do? Use the fitted model to classify each email in the dataset, and then calculate the classification error rates (TP, TN, FP, FN).

log_aug <- augment(log_fit2, email)


log_aug |>
  count(spam, .pred_class) |>
  group_by(spam) |>
  mutate(p = n / sum(n))

# A tibble: 4 × 4
# Groups:   spam [2]
  spam  .pred_class     n       p
  <fct> <fct>       <int>   <dbl>
1 0     0            3521 0.991  
2 0     1              33 0.00929
3 1     0             299 0.815  
4 1     1              68 0.185