AE 18: minimum wage

Card and Krueger (1994 AER) is a famous study on the impact of minimum wage increases on employment. The abstract reads:

On April 1, 1992, New Jersey’s minimum wage rose from $4.25 to $5.05 per hour. To evaluate the impact of the law we surveyed 410 fast-food restaurants in New Jersey and eastern Pennsylvania before and after the rise. Comparisons of employment growth at stores in New Jersey and Pennsylvania (where the minimum wage was constant) provide simple estimates of the effect of the higher minimum wage. We also compare employment changes at stores in New Jersey that were initially paying high wages (above $5) to the changes at lower-wage stores. We find no indication that the rise in the minimum wage reduced employment.

The data in Card and Krueger are purely observational, but the main idea is that the arbitrary placement of otherwise similar restaurants on either side of the PA/NJ border acts as if a controlled, randomized experiment were performed, and so we can use these data to draw causal conclusions about the impact of minimum wage policy on employment.

You already played with these data on Lab 5, but that was before we had begun working with multiple linear regression, and before we had studied statistical inference. So let us revisit this study with our new tools.

Packages

You know the drill:

Data

Load in dat data:

card_krueger <- read_csv("data/card-krueger.csv")

card_krueger <- card_krueger |>
  mutate(
    state = fct_relevel(state, "PA", "NJ")
  )

glimpse(card_krueger)
Rows: 351
Columns: 13
$ id          <dbl> 56, 61, 445, 451, 455, 458, 462, 468, 469, 470, 474, 481, …
$ chain       <chr> "Wendy's", "Wendy's", "Burger King", "Burger King", "KFC",…
$ co_owned    <dbl> 1, 1, 0, 0, 1, 1, 1, 0, 0, 0, 0, 1, 1, 1, 0, 0, 1, 1, 0, 1…
$ state       <fct> PA, PA, PA, PA, PA, PA, PA, PA, PA, PA, PA, PA, PA, PA, PA…
$ emp_diff    <dbl> -14.00, 11.50, -41.50, 13.00, 0.00, -0.50, 2.00, -29.00, 4…
$ wage_st     <dbl> 5.00, 5.50, 5.00, 5.00, 5.25, 5.00, 5.00, 5.00, 5.00, 5.50…
$ wage_st2    <dbl> 5.25, 4.75, 4.75, 5.00, 5.00, 5.00, 4.75, 5.00, 4.50, 4.75…
$ hrsopen     <dbl> 12.0, 12.0, 18.0, 24.0, 10.0, 10.0, 12.5, 18.0, 18.0, 18.0…
$ hrsopen2    <dbl> 12.0, 12.0, 18.0, 24.0, 11.0, 10.5, 12.0, 18.0, 18.0, 18.0…
$ fte         <dbl> 34.00, 24.00, 70.50, 23.50, 11.00, 9.00, 15.50, 58.00, 26.…
$ fte2        <dbl> 20.0, 35.5, 29.0, 36.5, 11.0, 8.5, 17.5, 29.0, 30.5, 26.0,…
$ meal_price  <dbl> 3.48, 3.29, 2.86, 2.85, 3.78, 3.99, 3.17, 2.84, 2.60, 2.75…
$ meal_price2 <dbl> 2.58, 2.80, 2.84, 2.89, 4.10, 3.95, 2.91, 2.67, 2.60, 2.81…

Variables include:

  • id: a unique identifier for each restaurant;
  • state: which state is the restaurant in?
  • chain: which restaurant chain does the store belong to?
  • co_owned: is the restaurant company owned?
  • wage_st and wage_st2: the starting wage in US dollars before and after policy change;
  • fte and fte2: full-time-equivalent employment before and after the change, calculated as the number of full-time workers (including managers) plus 0.5 times the number of part-time workers;
  • hrsopen and hrsopen2: number of hours open per day;
  • meal_price and meal_price2: the price of a meal (soda, fries, entree);
  • emp_diff: fte2-fte.

Question: are these data tidy?

Explore and visualize

The core claim of the study is that the two groups of restaurants are indistinguishable in all respects except for the minimum wage policy, and so any differences in employment can be ascribed to the causal impact of that policy. Let’s see how the states compare.

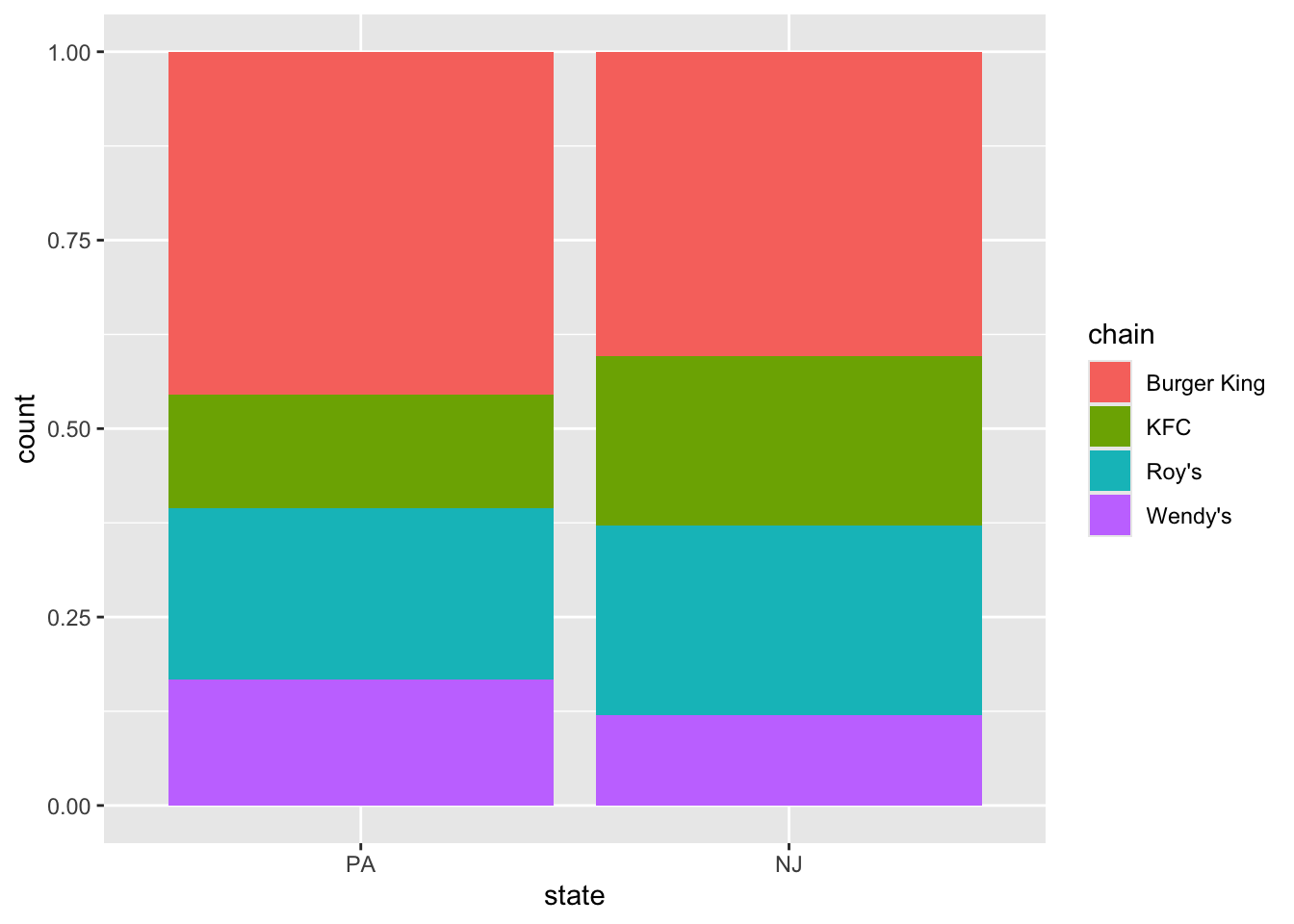
Compare chain composition

Do both states have roughly the same proportions of each restaurants in each chain? Create a figure that answers this question.

ggplot(card_krueger, aes(x = state, fill = chain)) + 
  geom_bar(position = "fill")

Same proportion of company owned?

card_krueger |>
  group_by(state) |>
  count(co_owned) |>
  mutate(
    prop = n / sum(n)
  )
# A tibble: 4 × 4
# Groups:   state [2]
  state co_owned     n  prop
  <fct>    <dbl> <int> <dbl>
1 PA           0    42 0.636
2 PA           1    24 0.364
3 NJ           0   185 0.649
4 NJ           1   100 0.351

Compare meal prices

How did the distribution of meal prices in each state compare before and after the policy change?

ggplot(card_krueger, aes(x = meal_price, color = state, fill = state)) +
  geom_density(alpha = 0.5) + 
  xlim(0, 6)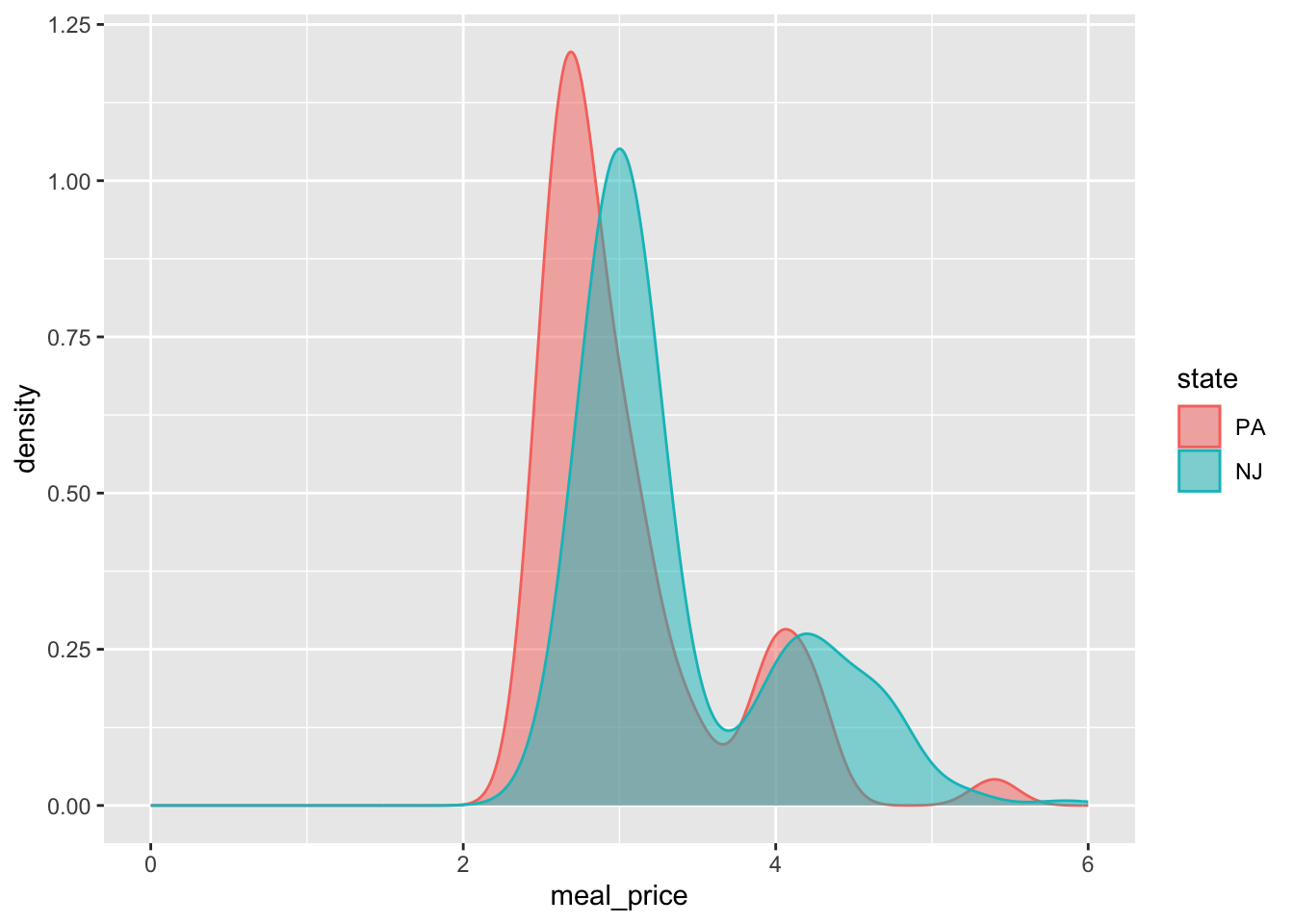

ggplot(card_krueger, aes(x = meal_price2, color = state, fill = state)) +
  geom_density(alpha = 0.5) + 
  xlim(0, 6)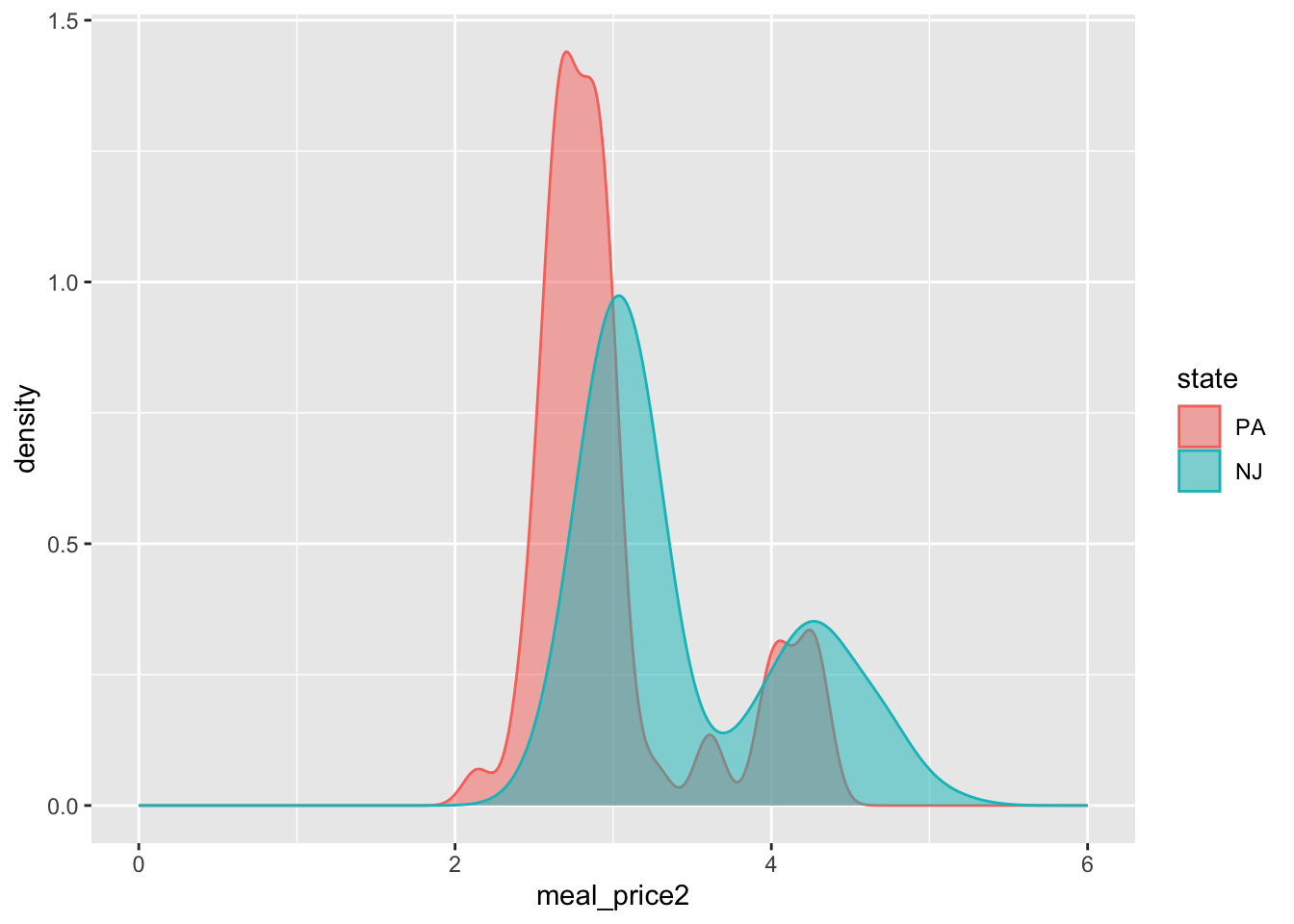

Investigate: Why is the distribution bimodal?

card_krueger |>
  filter(state == "NJ") |>
  ggplot(aes(x = meal_price, color = chain, fill = chain)) +
  geom_density(alpha = 0.5) + 
  xlim(0, 6)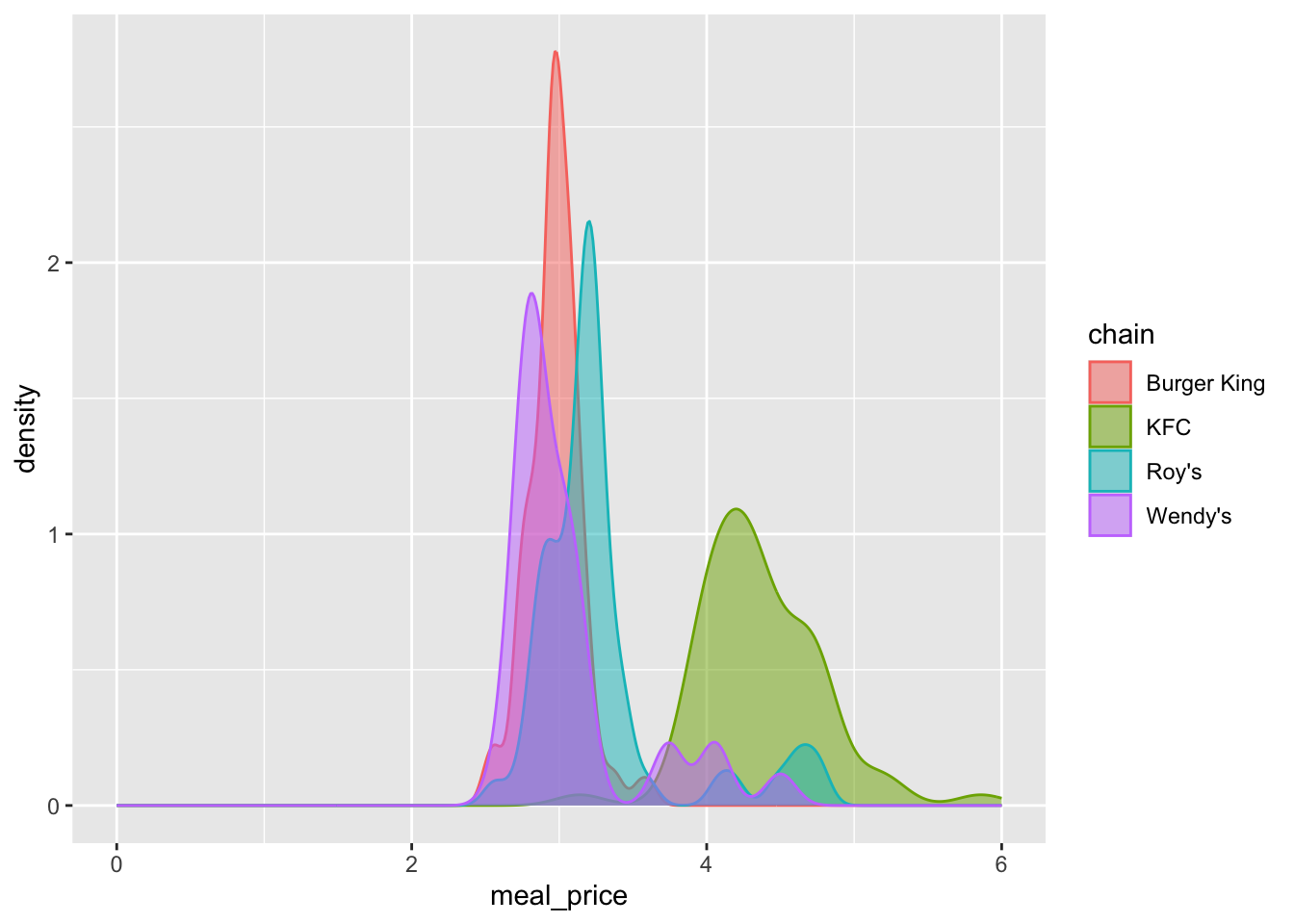

Point estimate

Here is the simple linear regression that you fit on Lab 5:

simple_fit <- linear_reg() |>
  fit(emp_diff ~ state, data = card_krueger)

tidy(simple_fit)
# A tibble: 2 × 5
  term        estimate std.error statistic p.value
  <chr>          <dbl>     <dbl>     <dbl>   <dbl>
1 (Intercept)    -1.88      1.07     -1.75  0.0807
2 stateNJ         2.28      1.19      1.91  0.0566

Fit an alternative model with multiple predictors

Fit a new model that controls for the restaurant chain and whether or not it is company owned:

multiple_fit <- linear_reg() |>
  fit(emp_diff ~ state + chain + co_owned, data = card_krueger)

tidy(multiple_fit)
# A tibble: 6 × 5
  term         estimate std.error statistic p.value
  <chr>           <dbl>     <dbl>     <dbl>   <dbl>
1 (Intercept)    -1.45       1.21    -1.20   0.232 
2 stateNJ         2.28       1.20     1.91   0.0575
3 chainKFC        0.235      1.30     0.181  0.857 
4 chainRoy's     -2.08       1.32    -1.58   0.116 
5 chainWendy's   -0.757      1.49    -0.507  0.612 
6 co_owned        0.373      1.10     0.339  0.735

Which model is “best”

glance(simple_fit)
# A tibble: 1 × 12
  r.squared adj.r.squared sigma statistic p.value    df logLik   AIC   BIC
      <dbl>         <dbl> <dbl>     <dbl>   <dbl> <dbl>  <dbl> <dbl> <dbl>
1    0.0104       0.00754  8.71      3.66  0.0566     1 -1257. 2520. 2532.
# ℹ 3 more variables: deviance <dbl>, df.residual <int>, nobs <int>
glance(multiple_fit)
# A tibble: 1 × 12
  r.squared adj.r.squared sigma statistic p.value    df logLik   AIC   BIC
      <dbl>         <dbl> <dbl>     <dbl>   <dbl> <dbl>  <dbl> <dbl> <dbl>
1    0.0204       0.00619  8.72      1.44   0.211     5 -1255. 2524. 2551.
# ℹ 3 more variables: deviance <dbl>, df.residual <int>, nobs <int>

The simpler model has higher adjusted \(R^2\), so we prefer it.

Interval estimate

Compute and visualize a 95% confidence interval for the change in average employment before and after the policy change:

empdiff_state_fit <- card_krueger |>
  specify(emp_diff ~ state) |>
  fit()

set.seed(8675309)
boot_fits <- card_krueger |>
  specify(emp_diff ~ state) |>
  generate(reps = 1000, type = "bootstrap") |>
  fit()

ci_90 <- get_confidence_interval(
  boot_fits,
  point_estimate = empdiff_state_fit,
  level = 0.90,
  type = "percentile"
)
ci_90
# A tibble: 2 × 3
  term      lower_ci upper_ci
  <chr>        <dbl>    <dbl>
1 intercept  -4.17      0.425
2 stateNJ    -0.0884    4.66 
visualize(boot_fits) + 
  shade_confidence_interval(ci_90)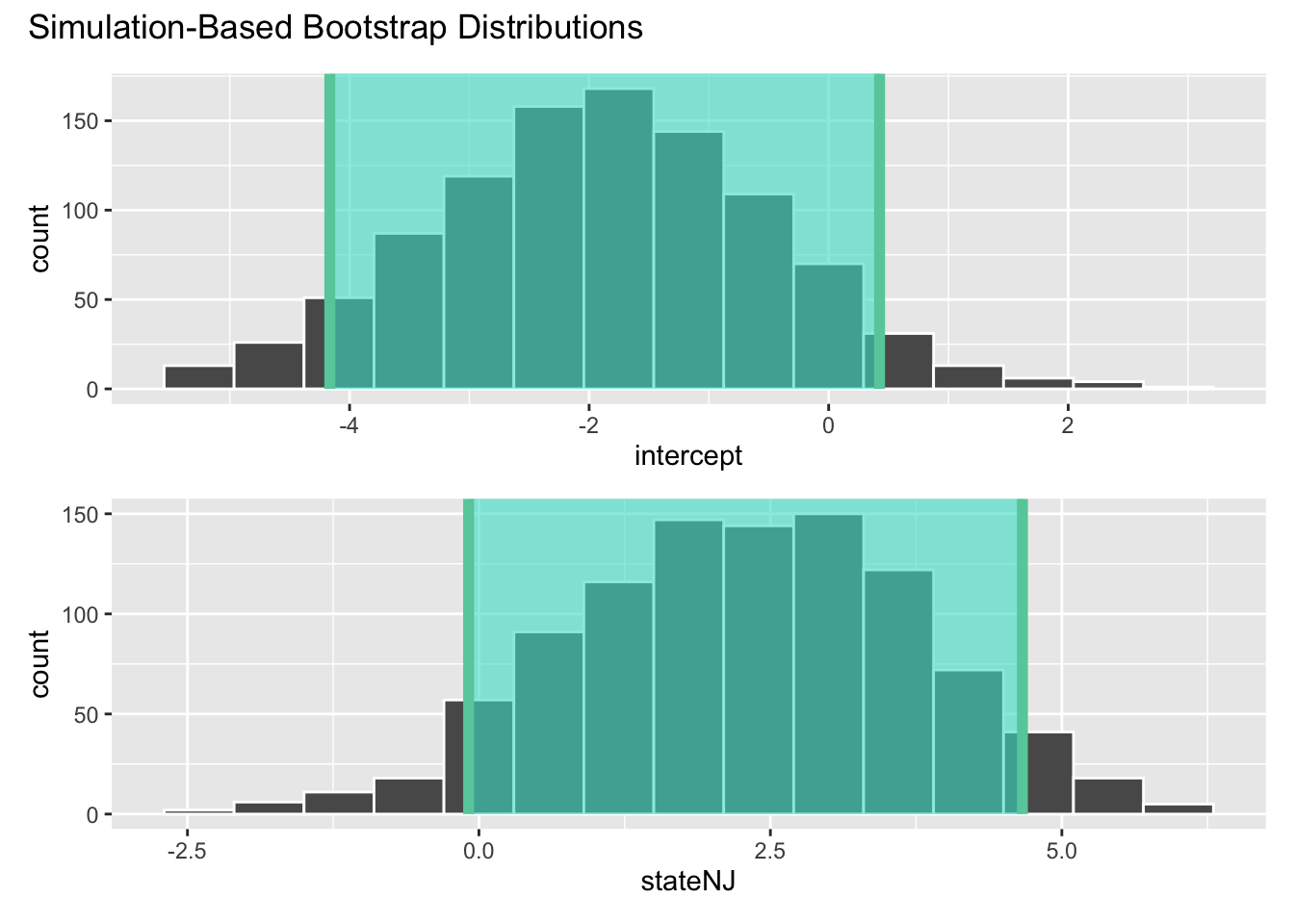

Hypothesis test

Test these hypotheses at a 5% discernibility level:

\[ \begin{aligned} H_0&: \beta_1=0 \quad(\text{no change})\\ H_0&: \beta_1\neq0 \quad(\text{some change}) \end{aligned} \]

Compute, visualize, and interpret the p-value.

set.seed(20)
null_dist <- card_krueger |>
  specify(emp_diff ~ state) |>
  hypothesize(null = "independence") |>
  generate(reps = 1000, type = "permute") |>
  fit()

visualize(null_dist) +
  shade_p_value(obs_stat = empdiff_state_fit, direction = "two-sided")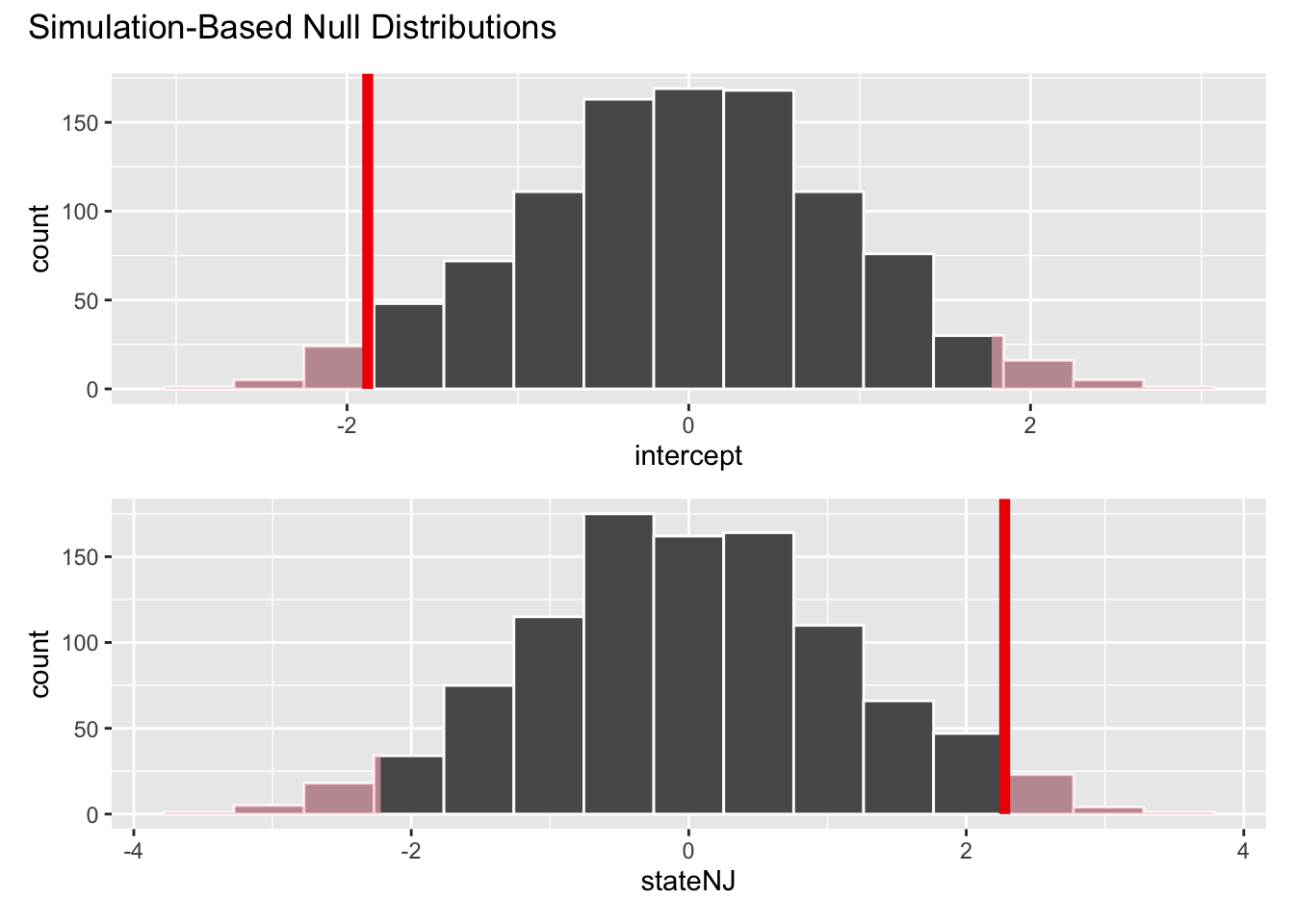

null_dist |>
  get_p_value(obs_stat = empdiff_state_fit, direction = "two-sided")
# A tibble: 2 × 2
  term      p_value
  <chr>       <dbl>
1 intercept   0.054
2 stateNJ     0.054

If the null hypothesis were true, the probability of a result as or more extreme than the one we computed would be 5.4%. So we just barely fail to reject the null at the 5% level.