Midterm 2 Practice Answers

  1. (c) For every additional $1,000 of annual salary, the model predicts the raise to be higher, on average, by 0.0155%.
  2. (d) \(R^2\) of raise_2_fit is higher than \(R^2\) of raise_1_fit since raise_2_fit has one more predictor and \(R^2\) always
  3. The reference level of performance_rating is High, since it’s the first level alphabetically. Therefore, the coefficient -2.40% is the predicted difference in raise comparing High to Successful. In this context a negative coefficient makes sense since we would expect those with High performance rating to get higher raises than those with Successful performance.
  4. (a) “Poor”, “Successful”, “High”, “Top”.
  5. Option 3. It’s a linear model with no interaction effect, so parallel lines. And since the slope for salary_typeSalaried is positive, its intercept is higher. The equations of the lines are as follows:

    • Hourly:

      \[ \begin{align*} \widehat{percent\_incr} &= 1.24 + 0.0000137 \times annual\_salary + 0.913 salary\_typeSalaried \\ &= 1.24 + 0.0000137 \times annual\_salary + 0.913 \times 0 \\ &= 1.24 + 0.0000137 \times annual\_salary \end{align*} \]

    • Salaried:

      \[ \begin{align*} \widehat{percent\_incr} &= 1.24 + 0.0000137 \times annual\_salary + 0.913 salary\_typeSalaried \\ &= 1.24 + 0.0000137 \times annual\_salary + 0.913 \times 1 \\ &= 2.153 + 0.0000137 \times annual\_salary \end{align*} \]

  6. (c) The model predicts that the percentage increase employees with Successful performance get, on average, is higher by a factor of 1025 compared to the employees with Poor performance rating.
  7. (d) as.numeric(str_remove(runtime, " mins"))
  8. (e) Blue City \(>\) Rang De Basanti \(>\) Winter Sleep
  9. (b) 31% of the variability in movie scores is explained by their runtime.
  10. (a) summarize
  11. (b) A value between 0 and 0.434.
  12. (e) G-rated movies that are 0 minutes in length are predicted to score, on average, 4.525 points.
  13. (c) All else held constant, for each additional minute of runtime, movie scores will be higher by 0.021 points on average.
  14. (c) is greater than
  15. (a) \(\widehat{score} = (4.525 - 0.257) + 0.021 \times runtime\)
  16. (a) and (d).
  17. (c) We are 95% confident that the mean number of texts per month of all American teens is between 1450 and 1550.
  18. A parsimonious model is the simplest model with the best predictive performance.
  19. a.

Spam is a factor; it is an indicator for if an email was spam or not.

email |> 
  count(spam) |>
  mutate(percent = (n/sum(n))*100)
# A tibble: 2 × 3
  spam      n percent
  <fct> <int>   <dbl>
1 0      3554   90.6 
2 1       367    9.36

About 9.36 percent of the emails are labeled spam.

b.
Dollar is a double.

email |>
  ggplot(aes(x = dollar)) + 
  geom_histogram(bins = 20) + 
  labs(
    title = "Histogram of dollar mentions in emails",
    x = "Number of times dollar appears in the email",
    y = "Count"
  )

email |>
  summarize(
    dollar_median = median(dollar),
    dollar_iqr = IQR(dollar),
    dollar_q25 = quantile(dollar, 0.25),
    dollar_q75 = quantile(dollar, 0.75)
  )
# A tibble: 1 × 4
  dollar_median dollar_iqr dollar_q25 dollar_q75
          <dbl>      <dbl>      <dbl>      <dbl>
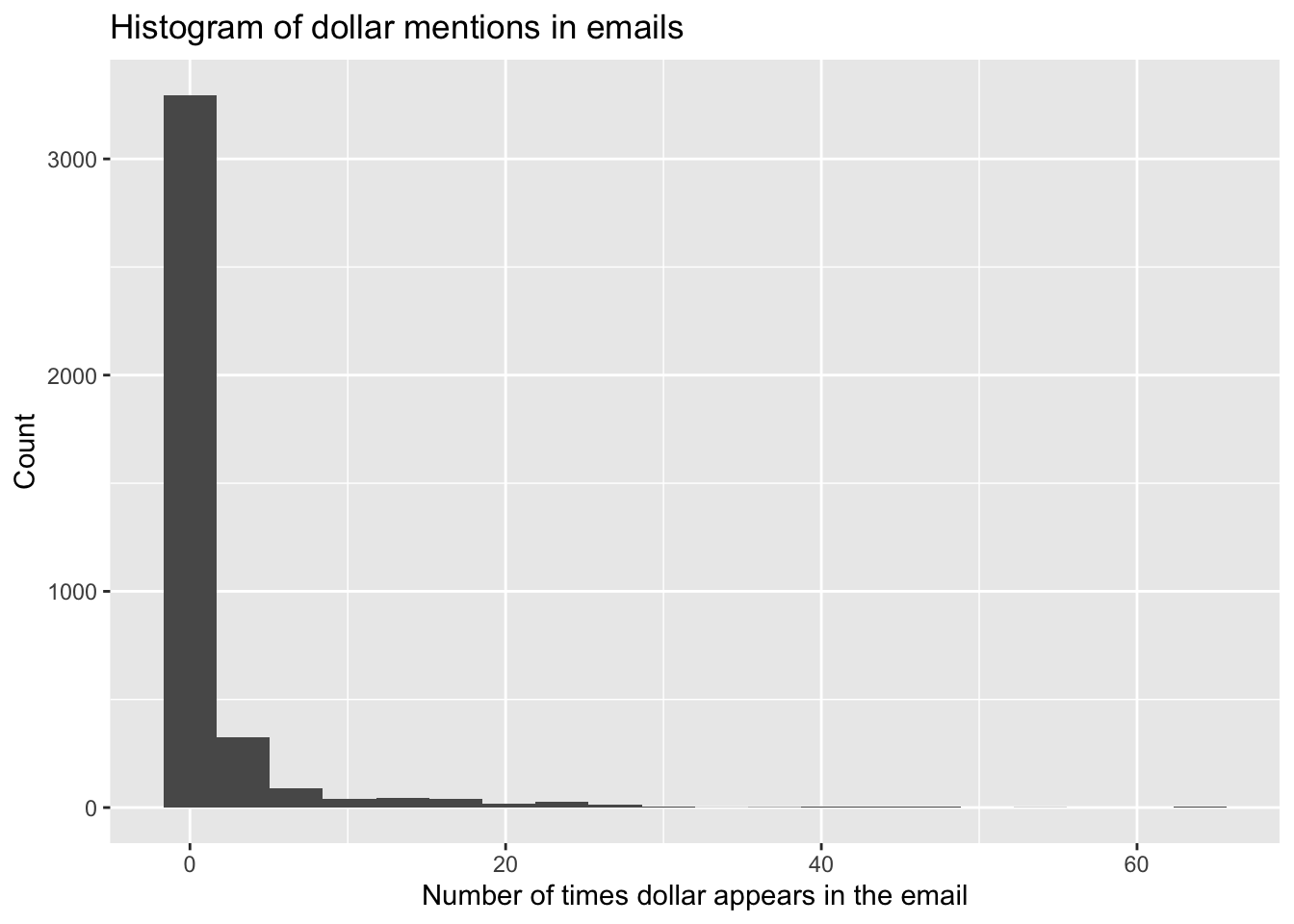
1             0          0          0          0

The distribution of dollar is unimodal and right-skewed with a median of 0. In fact, the majority of the emails have 0 dollar signs in them.

c.

spam_dollar_fit <- logistic_reg() |>
  fit(spam ~ dollar, data = email)

tidy(spam_dollar_fit)
# A tibble: 2 × 5
  term        estimate std.error statistic p.value
  <chr>          <dbl>     <dbl>     <dbl>   <dbl>
1 (Intercept)  -2.21      0.0569    -38.9  0      
2 dollar       -0.0564    0.0195     -2.89 0.00380

d.

The probability the email is spam in this case is 7.6%. Since it is less than 50% the email is classified as not spam.

new_email = tibble(dollar = 5)

predict(spam_dollar_fit, new_data = new_email, type = "prob")
# A tibble: 1 × 2
  .pred_0 .pred_1
    <dbl>   <dbl>
1   0.924  0.0763
  1. a.
spam_dollar_winner_urg_fit <- logistic_reg() |>
  fit(
    spam ~ dollar + winner + urgent_subj, 
    data = email
  )

tidy(spam_dollar_winner_urg_fit)
# A tibble: 4 × 5
  term         estimate std.error statistic  p.value
  <chr>           <dbl>     <dbl>     <dbl>    <dbl>
1 (Intercept)   -2.26      0.0581    -38.9  0       
2 dollar        -0.0663    0.0195     -3.40 6.86e- 4
3 winneryes      1.78      0.287       6.21 5.21e-10
4 urgent_subj1   2.61      0.767       3.40 6.75e- 4

b.

spam_dollar_winner_urg_aug <- augment(spam_dollar_winner_urg_fit, new_data = email)

spam_dollar_winner_urg_aug
# A tibble: 3,921 × 24
   .pred_class .pred_0 .pred_1 spam  to_multiple from     cc sent_email
   <fct>         <dbl>   <dbl> <fct> <fct>       <fct> <int> <fct>     
 1 0             0.906  0.0944 0     0           1         0 0         
 2 0             0.906  0.0944 0     0           1         0 0         
 3 0             0.926  0.0740 0     0           1         0 0         
 4 0             0.906  0.0944 0     0           1         0 0         
 5 0             0.906  0.0944 0     0           1         0 0         
 6 0             0.906  0.0944 0     0           1         0 0         
 7 0             0.906  0.0944 0     1           1         0 1         
 8 0             0.906  0.0944 0     1           1         1 1         
 9 0             0.906  0.0944 0     0           1         0 0         
10 0             0.906  0.0944 0     0           1         0 0         
# ℹ 3,911 more rows
# ℹ 16 more variables: time <dttm>, image <dbl>, attach <dbl>, dollar <dbl>,
#   winner <fct>, inherit <dbl>, viagra <dbl>, password <dbl>, num_char <dbl>,
#   line_breaks <int>, format <fct>, re_subj <fct>, exclaim_subj <dbl>,
#   urgent_subj <fct>, exclaim_mess <dbl>, number <fct>

c.

email_pred_counts <- spam_dollar_winner_urg_aug |>
  count(spam, .pred_class)

email_pred_counts
# A tibble: 4 × 3
  spam  .pred_class     n
  <fct> <fct>       <int>
1 0     0            3551
2 0     1               3
3 1     0             363
4 1     1               4

There are 4 emails that are spam and are correctly identified. There are 363 emails that are spam that are labelled as not spam. There are 3 emails that are not spam that are labelled as spam. There are 3551 emails that are not spam and are correctly identified.

d.

The false positive rate is 0.0844% and false negative rate is 98.9%.

email_pred_counts |>
  group_by(spam) |>
  mutate(p = n / sum(n))
# A tibble: 4 × 4
# Groups:   spam [2]
  spam  .pred_class     n        p
  <fct> <fct>       <int>    <dbl>
1 0     0            3551 0.999   
2 0     1               3 0.000844
3 1     0             363 0.989   
4 1     1               4 0.0109
  1. a.
email |>
  ggplot(aes(x = num_char, y = spam)) +
  geom_boxplot() + 
  labs(
    title = "Boxplot of number of characters for spam and not spam emails",
    x = "Number of characters",
    y = "Spam"
  )

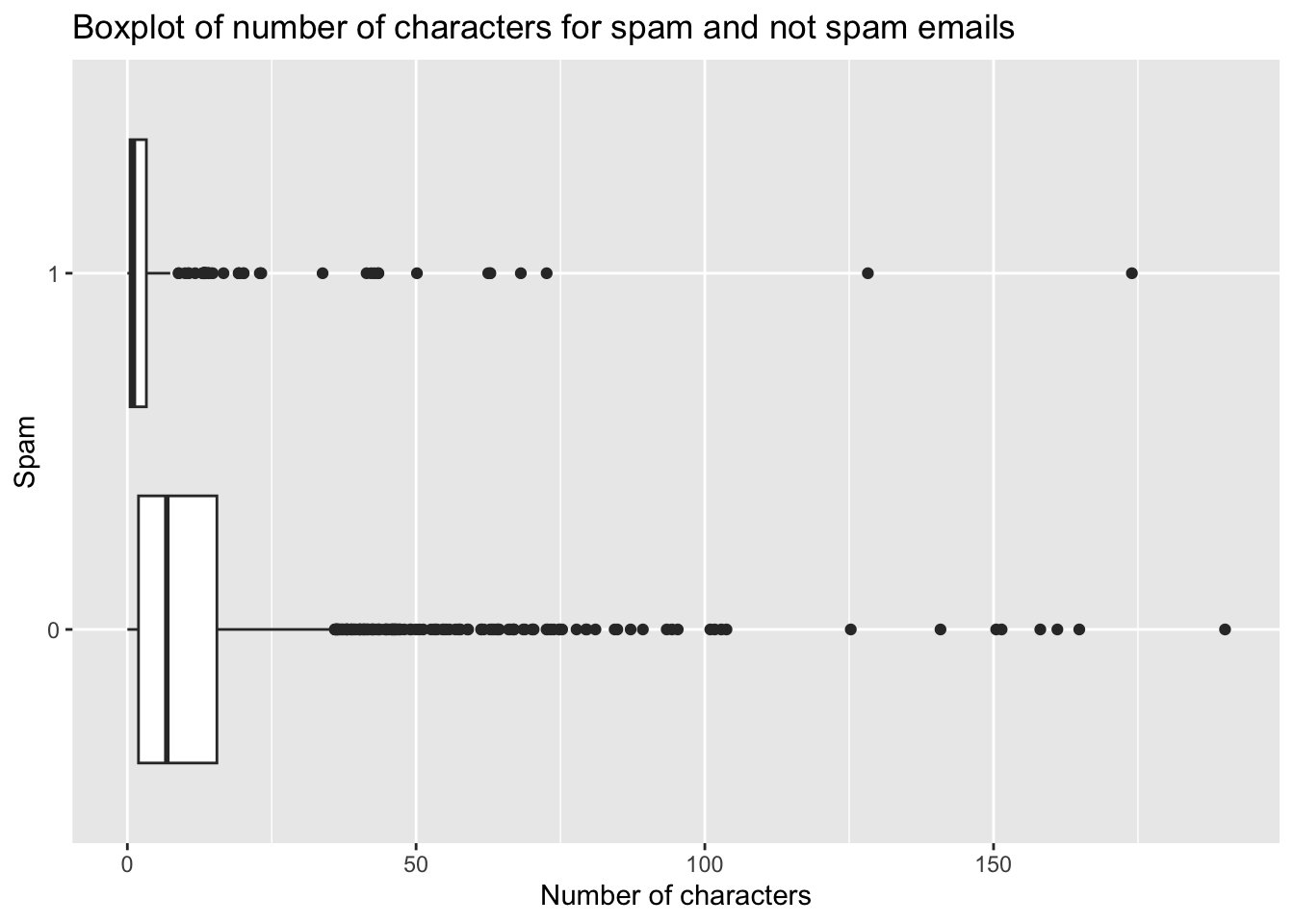
Number of characters could be reasonable predictor of spam. Also, this plot supports differences in distributions. (I also included the predictors from Question 2 – winner and urgent_subj in addition to dollar)

spam_dollar_char_fit <- logistic_reg() |>
  fit(
    spam ~  dollar + winner + urgent_subj + num_char, 
    data = email
  )

tidy(spam_dollar_char_fit)
# A tibble: 5 × 5
  term         estimate std.error statistic   p.value
  <chr>           <dbl>     <dbl>     <dbl>     <dbl>
1 (Intercept)   -1.84     0.0724     -25.5  4.23e-143
2 dollar        -0.0206   0.0203      -1.02 3.10e-  1
3 winneryes      2.01     0.303        6.62 3.62e- 11
4 urgent_subj1   2.31     0.772        3.00 2.74e-  3
5 num_char      -0.0619   0.00835     -7.41 1.26e- 13

b.

spam_dollar_char_fit_aug <- augment(spam_dollar_char_fit, new_data = email)

c.

pred_counts <- spam_dollar_char_fit_aug |>
  count(spam, .pred_class)
pred_counts
# A tibble: 4 × 3
  spam  .pred_class     n
  <fct> <fct>       <int>
1 0     0            3547
2 0     1               7
3 1     0             353
4 1     1              14

d.

The false negative rate decreased to 96.2%. The false positive rate is a tiny bit higher at 0.2%.

pred_counts |>
  group_by(spam) |>
  mutate(p = n / sum(n))
# A tibble: 4 × 4
# Groups:   spam [2]
  spam  .pred_class     n       p
  <fct> <fct>       <int>   <dbl>
1 0     0            3547 0.998  
2 0     1               7 0.00197
3 1     0             353 0.962  
4 1     1              14 0.0381

e. The model from Question 21 is preferable over the model in Question 20. While the false positive rate increased, the false negative rate decreased by a larger amount; and overall more emails are categorized correctly (3547+14 = 3561 emails vs 3551 + 4 = 3555) for the model used in Question 21.